Wortel Tot De Macht 3: Ontdek De Magie Van Drievoudige Wortels
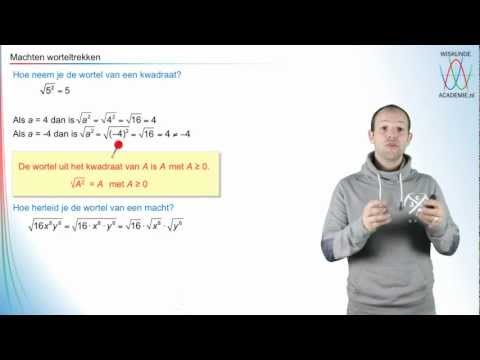
Wortels En Machten – Hoe Herleid Je Een Wortel Van Een Macht? (Havo/Vwo 2) – Wiskundeacademie
Keywords searched by users: wortel tot de macht 3 wortel tot de macht 3 rekenmachine, wortel is tot de macht 1/2, derdemachtswortel van 216, derdemachtswortel symbool, derdemachtswortel van 125, derdemachtswortel excel, derdemachtswortel van 5, derdemachtswortel rekenmachine ti-84
Wat is wortel tot de macht 3?
Wortel tot de macht 3, ook wel bekend als de derdemachtswortel, is een wiskundige bewerking waarbij je berekent welk getal tot de derde macht een specifiek getal oplevert. Met andere woorden, het is het tegenovergestelde van machtsverheffen tot de derde macht. Ter illustratie, als je het getal 2 tot de derde macht verheft, krijg je 8. De derdemachtswortel van 8 is 2, omdat 2 tot de derde macht gelijk is aan 8.
De derdemachtswortel is dus de inverse operatie van machtsverheffen tot de derde macht. Het stelt ons in staat om een getal te vinden dat, als we het tot de derde macht verheffen, het oorspronkelijke getal oplevert.
Hoe bereken je wortel tot de macht 3?
Om de derdemachtswortel van een getal te berekenen, kun je gebruik maken van een rekenmachine met een wortel tot de macht 3-functie. Deze functie neemt een getal als invoer en geeft het resultaat van de derdemachtswortel van dat getal als output. Je kunt ook gebruik maken van handmatige methoden, zoals schatten, om een benadering van de derdemachtswortel te vinden.
Een andere manier om de derdemachtswortel te berekenen, is door gebruik te maken van de exponentiële notatie. Als je bijvoorbeeld de derdemachtswortel van 8 wilt berekenen, kun je dit schrijven als 8^(1/3). Dit betekent dat je het getal 8 tot de macht van 1/3 moet verheffen. Het resultaat is 2, omdat 2 x 2 x 2 gelijk is aan 8.
Wat is de derdemachtswortel?
De derdemachtswortel is een wiskundige bewerking die ons in staat stelt om een getal te vinden dat, als we het tot de derde macht verheffen, het oorspronkelijke getal oplevert. De derdemachtswortel is de inverse bewerking van machtsverheffen tot de derde macht. Het is een belangrijk concept in de wiskunde en wordt vaak gebruikt in verschillende toepassingen, zoals het oplossen van vergelijkingen en het analyseren van complexe problemen.
Hoe kan de derdemachtswortel worden uitgedrukt in wiskundige notatie?
De derdemachtswortel kan worden uitgedrukt in wiskundige notatie als het getal tot de macht van 1/3. Bijvoorbeeld, de derdemachtswortel van 8 kan worden geschreven als 8^(1/3), waarbij het getal 8 tot de macht van 1/3 moet worden verheven.
Daarnaast wordt de derdemachtswortel soms ook aangeduid met het symbool voor wortel met een klein 3’tje in de linkerbovenhoek van het radicaalteken (∛). Dit symbool wordt gebruikt om aan te geven dat we op zoek zijn naar de derdemachtswortel van een bepaald getal.
Praktische voorbeelden van wortel tot de macht 3
Laten we eens kijken naar enkele praktische voorbeelden om het concept van wortel tot de macht 3 beter te begrijpen.
Voorbeeld 1:
Laten we de derdemachtswortel van 27 berekenen. We kunnen dit schrijven als 27^(1/3). Het resultaat is 3, omdat 3 x 3 x 3 gelijk is aan 27.
Voorbeeld 2:
Laten we de derdemachtswortel van 64 berekenen. We kunnen dit schrijven als 64^(1/3). Het resultaat is 4, want 4 x 4 x 4 is gelijk aan 64.
Voorbeeld 3:
Stel dat we de derdemachtswortel van -8 willen berekenen. In dit geval moeten we ons bewust zijn van het feit dat we alleen de derdemachtswortel kunnen berekenen van positieve getallen. De derdemachtswortel van -8 is dus niet gedefinieerd in de reële getallen.
Waarom is wortel tot de macht 3 een belangrijk concept in de wiskunde?
Wortel tot de macht 3 is een belangrijk concept in de wiskunde omdat het ons in staat stelt om de inverse operatie uit te voeren van machtsverheffen tot de derde macht. Het biedt ons een manier om oorspronkelijke getallen te herstellen en vergemakkelijkt het oplossen van vergelijkingen en het analyseren van complexe vraagstukken.
Daarnaast heeft de derdemachtswortel ook toepassingen in verschillende disciplines, zoals engineering, natuurkunde en economie. Het stelt professionals in staat om complexe berekeningen uit te voeren en oplossingen te vinden voor problemen die anders moeilijk te begrijpen zouden zijn.
FAQs
1. Wat is een derdemachtswortel rekenmachine?
Een derdemachtswortel rekenmachine is een rekenmachine die is uitgerust met een functie om de derdemachtswortel van een getal te berekenen. Met behulp van deze rekenmachine kunt u snel en nauwkeurig de derdemachtswortel van een getal berekenen zonder veel handmatige berekeningen te hoeven doen.
2. Wat betekent wortel tot de macht 1/2?
Wortel tot de macht 1/2, ook bekend als de vierkantswortel, is een bewerking waarbij je berekent welk getal tot de tweede macht een specifiek getal oplevert. Het is een speciaal geval van wortel tot de macht 3, waarbij de macht gelijk is aan 1/2 in plaats van 3.
3. Wat is de derdemachtswortel van 216?
De derdemachtswortel van 216 is 6. Dit komt omdat 6 x 6 x 6 gelijk is aan 216.
4. Wat is het symbool voor derdemachtswortel?
Het symbool voor derdemachtswortel is een radicaalteken (∛) met een klein 3’tje in de linkerbovenhoek om aan te geven dat we op zoek zijn naar de derdemachtswortel van een specifiek getal.
5. Wat is de derdemachtswortel van 125?
De derdemachtswortel van 125 is 5. Dit komt omdat 5 x 5 x 5 gelijk is aan 125.
6. Hoe bereken ik de derdemachtswortel in Excel?
Om de derdemachtswortel in Excel te berekenen, kunt u gebruik maken van de formule “=MACHTE.P(CELREFERENTIE;1/3)”. Vervang “CELREFERENTIE” door de cel waarin het getal staat waarvan u de derdemachtswortel wilt berekenen.
7. Wat is de derdemachtswortel van 5?
De derdemachtswortel van 5 is een irrationeel getal en kan niet exact worden uitgedrukt als een eindig decimaal getal of breuk. Het kan worden benaderd als 1,70997594668.
8. Hoe gebruik ik een derdemachtswortel rekenmachine TI-84?
Op een TI-84 rekenmachine kunt u de derdemachtswortel berekenen door het getal in te voeren en vervolgens op de knop “^” te drukken, gevolgd door het invoeren van “1/3”. Druk op de “ENTER” knop om het resultaat te krijgen.
Om een derdemachtswortel te vinden met het symbool, kunt u ook de “Math” knop indrukken, en vervolgens “∛” selecteren, gevolgd door het getal dat u wilt vinden de derdemachtswortel van. Druk op “ENTER” om het resultaat te krijgen.
Dit zijn enkele voorbeelden van hoe wortel tot de macht 3 kan worden gebruikt en berekend. Het is een belangrijk concept in de wiskunde en kan de deur openen naar het oplossen van verschillende wiskundige vraagstukken en praktische problemen.
Categories: Details 57 Wortel Tot De Macht 3
Wortel Tot De Macht 3 Rekenmachine
Het berekenen van wortels en machten is een essentiële vaardigheid in de wiskunde. Een bijzondere bewerking is het nemen van de derdemachtswortel, ofwel de wortel tot de macht 3, van een getal. In dit artikel zullen we dieper ingaan op de wortel tot de macht 3 rekenmachine en u voorzien van gedetailleerde informatie en uitleg over dit onderwerp.
## Wat is de Wortel tot de Macht 3?
De wortel tot de macht 3 van een getal houdt in dat we het getal moeten vinden dat, wanneer het tot de derde macht wordt verheven, gelijk is aan het originele getal. Met andere woorden, we zoeken naar het getal waarvan het resultaat na verheffing tot de derde macht gelijk is aan het oorspronkelijke getal. Dit concept wordt aangeduid met het wiskundige symbool ∛.
## Berekening van de Wortel tot de Macht 3
Het berekenen van de wortel tot de macht 3 kan handmatig worden gedaan, maar het kan tijdrovend en complex zijn, vooral voor grote getallen. Daarom is het handig om gebruik te maken van een rekenmachine die is ontworpen om deze bewerking snel en nauwkeurig uit te voeren.
Gelukkig zijn er online rekenmachines beschikbaar die speciaal zijn ontwikkeld voor het berekenen van de wortel tot de macht 3. Deze rekenmachines accepteren een invoergetal en geven direct het resultaat van de berekening. Dit maakt het proces veel sneller en efficiënter.
## Hoe Werkt de Wortel tot de Macht 3 Rekenmachine?
De wortel tot de macht 3 rekenmachine maakt gebruik van geavanceerde wiskundige algoritmes en formules om de berekening uit te voeren. Het werkt als volgt:
1. Voer het gewenste getal in dat u wilt verheffen tot de derde macht.
2. Druk op de enterknop of klik op de berekenknop.
3. De rekenmachine zal het resultaat tonen, dat gelijk is aan de wortel tot de macht 3 van het ingevoerde getal.
Met behulp van de wortel tot de macht 3 rekenmachine kunt u snel en gemakkelijk de derdemachtswortel van elk willekeurig getal berekenen. Dit kan handig zijn bij het oplossen van wiskundige problemen, het maken van wetenschappelijke berekeningen of het uitvoeren van complexe formules.
## Veel Gestelde Vragen (FAQ)
Hier zijn enkele veelvoorkomende vragen over de wortel tot de macht 3 rekenmachine:
Q: Waar kan ik een online wortel tot de macht 3 rekenmachine vinden?
A: Er zijn verschillende websites en online tools beschikbaar die u kunnen helpen bij het berekenen van de wortel tot de macht 3. Enkele populaire opties zijn Calculator.net, Symbolab en Mathway.
Q: Kunnen rekenmachines de wortel tot de macht 3 van negatieve getallen berekenen?
A: Ja, de meeste rekenmachines kunnen ook de wortel tot de macht 3 van negatieve getallen berekenen. Het resultaat zal echter een complex getal zijn, aangezien er geen reëel getal is dat bij verheffing tot de derde macht een negatief getal oplevert.
Q: Kan ik een wortel tot de macht 3 berekening uitvoeren op mijn grafische rekenmachine?
A: Ja, de meeste geavanceerde grafische rekenmachines hebben de mogelijkheid om de wortel tot de macht 3 van een getal te berekenen. Raadpleeg de handleiding van uw specifieke rekenmachine om te achterhalen hoe u deze bewerking kunt uitvoeren.
Q: Wat zijn enkele toepassingen van de wortel tot de macht 3?
A: De wortel tot de macht 3 wordt vaak gebruikt bij het oplossen van wiskundige vergelijkingen en problemen waarbij een derdemachtswortel nodig is. Het kan ook van pas komen in de natuurkunde, engineering en andere wetenschappelijke disciplines.
## Conclusie
De wortel tot de macht 3 rekenmachine is een handige tool waarmee u snel en nauwkeurig de derdemachtswortel van een getal kunt berekenen. Het maakt gebruik van geavanceerde algoritmes en formules om de berekening uit te voeren en geeft direct het resultaat weer. Of u nu een wiskundige vergelijking oplost of wetenschappelijke berekeningen uitvoert, de wortel tot de macht 3 rekenmachine kan u helpen bij het vereenvoudigen van complexe bewerkingen. Probeer het zelf uit en ontdek hoe handig deze rekenmachine kan zijn!
Referentiematerialen:
– [Wikipedia: Derdemachtswortel](https://nl.wikipedia.org/wiki/Derdemachtswortel)
– [Wat zijn hogeremachtswortels? – Mr. Chadd Academy](https://www.mrchadd.nl/academy/vakken/wiskunde/wat-zijn-hogeremachtswortels)
– [Wat is de wortel van 9 tot de macht 3X](https://studygo.com/nl/learn/question/336163/wat-is-de-de-wortel-van-9-tot-de-macht-3x)
– [Hoeveel is de wortel van drie met de macht van 3?](https://studygo.com/nl/learn/question/132056/hoeveel-is-de-wortel-van-drie-met-de-macht-van-3-)
– [De derdemachtswortel van een geheel getal](https://uva.sowiso.nl/courses/theory/7/82/10076/nl)
– [Wortels – Theorie wiskunde](https://www.dr-aart.nl/Rekenen-wortels.html)
Wortel Is Tot De Macht 1/2
Als het gaat om wiskundige berekeningen, kunnen exponenten en wortels soms verwarrend lijken. Een onderwerp dat speciale aandacht verdient, is de wortel tot de macht 1/2. In dit artikel zullen we dieper ingaan op dit concept, de toepassingen ervan en hoe het relevant kan zijn in wiskundige berekeningen. Laten we beginnen!
### Inleiding tot wortels
Voordat we duiken in de wortel tot de macht 1/2, laten we eerst een korte introductie geven tot wortels in het algemeen. Een wortel van een getal is een ander getal dat, wanneer vermenigvuldigd met zichzelf, het oorspronkelijke getal oplevert. Laten we als voorbeeld de wortel nemen van het getal 16. De wortel van 16 is 4, omdat 4 * 4 gelijk is aan 16.
In de wiskunde wordt een wortel aangeduid met het symbool √, wat vaak wordt uitgesproken als “wortel van”. Dus de wortel van 16 wordt geschreven als √16. In dit geval is de wortel 4.
### Machten en exponenten
Naast wortels is het ook belangrijk om te begrijpen wat machten en exponenten zijn. Een macht is het resultaat van het vermenigvuldigen van een getal met zichzelf een bepaald aantal keren. Dit aantal keren wordt een exponent genoemd.
Bijvoorbeeld, in de uitdrukking 2^3, waarbij het symbool ^ aangeeft dat het getal 2 wordt verheven tot de macht van 3, betekent dit dat we 2 vermenigvuldigen met zichzelf 3 keer:
2 * 2 * 2 = 8.
Dus 2^3 is gelijk aan 8.
### De wortel tot de macht 1/2
Nu we een basisuitleg hebben gegeven van wortels en machten, kunnen we verder gaan met het bespreken van de wortel tot de macht 1/2. Deze specifieke macht is een manier om de vierkantswortel uit een getal te berekenen.
Laten we als voorbeeld de wortel van 25 nemen, geschreven als √25. Om de wortel tot de macht 1/2 te berekenen, verheffen we 25 tot de macht van 1/2:
√25^1/2 = (25^1/2)^1/2.
Het uitvoeren van deze berekening geeft ons:
√25^1/2 = 5.
Dus de wortel tot de macht 1/2 van 25 is gelijk aan 5.
In het algemeen kunnen we zeggen dat de wortel tot de macht 1/2 van een getal x gelijk is aan de waarde van x tot de macht 1/2. Dit betekent dat de wortel tot de macht 1/2 van x kan worden geschreven als x^1/2.
### Toepassingen van de wortel tot de macht 1/2
Nu we weten hoe de wortel tot de macht 1/2 wordt berekend, laten we eens kijken naar enkele toepassingen ervan.
– Het is nuttig bij het oplossen van vergelijkingen waarin wortels voorkomen. Door de wortel tot de macht 1/2 te nemen, kunnen we een vergelijking herschrijven in een vorm die gemakkelijker op te lossen is.
– In de natuurkunde wordt de wortel tot de macht 1/2 vaak gebruikt bij het berekenen van de snelheid, versnelling en afstand van een object. Bijvoorbeeld, de snelheid van een object kan worden berekend door de wortel van de verhouding tussen de afgelegde afstand en de tijd te nemen.
– In de financiële wereld kan de wortel tot de macht 1/2 worden gebruikt bij het berekenen van rendementen op investeringen. Het kan helpen bij het bepalen van het gemiddelde rendement over een bepaalde periode.
Dit zijn slechts enkele voorbeelden van hoe de wortel tot de macht 1/2 kan worden toegepast. Het is een krachtig wiskundig concept dat in veel verschillende domeinen van toepassing is.
### Veelgestelde vragen (FAQ)
Hier zijn enkele veelgestelde vragen over de wortel tot de macht 1/2:
Q: Wat is het verschil tussen de wortel tot de macht 1/2 en de wortel tot de macht 1/3?
A: De wortel tot de macht 1/2 berekent de vierkantswortel van een getal, terwijl de wortel tot de macht 1/3 de derdemachtswortel van een getal berekent.
Q: Kan de wortel tot de macht 1/2 van een negatief getal worden berekend?
A: Nee, de wortel tot de macht 1/2 is alleen gedefinieerd voor niet-negatieve getallen. Voor negatieve getallen is de wortel niet reëel.
Q: Hoe kan de wortel tot de macht 1/2 worden gebruikt in complexe getallen?
A: In complexe getallen kan de wortel tot de macht 1/2 worden gebruikt bij het vinden van de wortels van een complex getal. Het resultaat zal bestaan uit twee complexe getallen.
Q: Kan de wortel tot de macht 1/2 worden toegepast op irrationale getallen?
A: Ja, de wortel tot de macht 1/2 kan worden toegepast op irrationale getallen. Het resultaat zal meestal ook een irrationaal getal zijn.
Q: Hoe kunnen we de wortel tot een andere macht dan 1/2 berekenen?
A: Om de wortel tot een andere macht dan 1/2 te berekenen, verheffen we het getal tot de macht van de gekozen wortel. Bijvoorbeeld, de derdemachtswortel van een getal x kan worden berekend als x^1/3.
### Conclusie
De wortel is tot de macht 1/2 is een belangrijk wiskundig concept dat ons in staat stelt de vierkantswortel van een getal te berekenen. Het kan worden toegepast in verschillende domeinen, zoals vergelijkingen, natuurkunde en financiën. Door de wortel tot de macht 1/2 te begrijpen, kunnen we complexe berekeningen vereenvoudigen en gemakkelijker maken. Hopelijk heeft dit artikel geholpen bij het verhelderen van dit onderwerp en het bieden van een diepgaand inzicht in de wortel tot de macht 1/2.
Derdemachtswortel Van 216
De derdemachtswortel van een getal is een wiskundige bewerking die veel voorkomt in verschillende toepassingen, zoals algebra, meetkunde en natuurkunde. In dit artikel zullen we ons richten op de derdemachtswortel van het getal 216, ook wel bekend als de kubieke wortel van 216. We zullen in detail uitleggen wat de derdemachtswortel precies is, hoe deze berekend kan worden en wat de toepassingen zijn van deze wiskundige bewerking. Daarnaast zullen we ook veelgestelde vragen beantwoorden om uw begrip van het onderwerp te vergroten.
Wat is de derdemachtswortel?
De derdemachtswortel van een getal is het getal dat, wanneer tot de derde macht wordt verheven, gelijk is aan het gegeven getal. Met andere woorden, de derdemachtswortel van een getal x kan worden berekend door te zoeken naar een ander getal y waarvoor geldt y * y * y = x. Dit kan worden geschreven als y³ = x.
In het geval van de derdemachtswortel van 216, zoeken we naar het getal y waarvoor y * y * y gelijk is aan 216. Met andere woorden, we zoeken naar een getal dat verheven tot de derde macht 216 oplevert.
Hoe bereken je de derdemachtswortel van 216?
Er zijn verschillende manieren om de derdemachtswortel van 216 te berekenen. Een veelgebruikte methode is door gebruik te maken van de rekenmachine of een wiskundig softwareprogramma. Hiermee kunt u de kubieke wortel van 216 nauwkeurig berekenen.
Een andere methode om de derdemachtswortel te benaderen is door gebruik te maken van de zogenaamde “radicaalnotatie”. De derdemachtswortel van 216 kan geschreven worden als ∛216. Door middel van opeenvolgende schattingen en iteraties kunt u een benadering van de kubieke wortel van 216 krijgen. Deze methode is echter tijdrovend en vereist enige wiskundige kennis en vaardigheden.
In het geval van de derdemachtswortel van 216 is de exacte waarde 6. Dit betekent dat 6 * 6 * 6 gelijk is aan 216.
Waarom is de derdemachtswortel van 216 gelijk aan 6?
Om te begrijpen waarom de derdemachtswortel van 216 gelijk is aan 6, moeten we de wiskundige berekening van de derdemachtswortel begrijpen. De derdemachtswortel is een vorm van worteltrekking, waarbij het getal wordt ontleed in zijn factoren.
216 kan worden geschreven als het product van drie factoren, namelijk 6 * 6 * 6. Daarom kan de derdemachtswortel van 216 worden geschreven als de wortel van 6 * 6 * 6. Omdat dezelfde factor, namelijk 6, drie keer wordt vermenigvuldigd, is de derdemachtswortel van 216 gelijk aan het enkele getal 6.
Toepassingen van de derdemachtswortel
De derdemachtswortel heeft verschillende toepassingen in de wiskunde en andere wetenschappelijke disciplines. Een van de belangrijkste toepassingen is te vinden in de algebra, waarbij de derdemachtswortel wordt gebruikt om vergelijkingen op te lossen. In driedimensionale meetkunde kan de derdemachtswortel worden gebruikt om de zijden van een kubus te berekenen.
Daarnaast komt de derdemachtswortel ook voor in natuurkundige formules. Bijvoorbeeld, in de formule voor het volume van een bol, wordt de derdemachtswortel gebruikt om de straal van de bol te berekenen op basis van het gegeven volume.
Veelgestelde vragen
1. Wat is de derdemachtswortel van 8?
De derdemachtswortel van 8 is gelijk aan 2. Dit kan worden berekend door te zoeken naar een getal dat verheven tot de derde macht 8 oplevert.
2. Wat is het verschil tussen de vierkantswortel en de derdemachtswortel?
De vierkantswortel is een wiskundige bewerking waarbij het getal wordt ontleed in twee factoren, terwijl de derdemachtswortel het getal ontleedt in drie factoren. De vierkantswortel wordt gebruikt om de lengte van een zijde van een vierkant te berekenen, terwijl de derdemachtswortel wordt gebruikt voor het berekenen van de zijden van een kubus.
3. Zijn er negatieve derdemachtswortels?
Ja, er zijn negatieve derdemachtswortels. Bijvoorbeeld, de derdemachtswortel van -8 is gelijk aan -2. Dit komt doordat (-2) * (-2) * (-2) gelijk is aan -8.
4. Is de derdemachtswortel van elk getal een geheel getal?
Nee, de derdemachtswortel van elk getal is niet per se een geheel getal. In veel gevallen zal de derdemachtswortel een decimaal getal zijn. Echter, als het gegeven getal een perfecte derdemacht is, dan zal de derdemachtswortel een geheel getal zijn.
Conclusie
De derdemachtswortel is een belangrijk concept in de wiskunde, met verschillende toepassingen in diverse wetenschappelijke gebieden. In dit artikel hebben we de derdemachtswortel van 216 besproken, waarbij we hebben uitgelegd wat de derdemachtswortel precies is, hoe deze berekend kan worden en waarom de derdemachtswortel van 216 gelijk is aan 6. We hebben ook enkele veelgestelde vragen beantwoord om uw begrip van het onderwerp te vergroten. Hopelijk heeft dit artikel bijgedragen aan uw kennis van de derdemachtswortel van 216.
Update 18 wortel tot de macht 3







See more here: toplist.prairiehousefreeman.com
Learn more about the topic wortel tot de macht 3.
- Derdemachtswortel
- Wat zijn hogeremachtswortels? – Mr. Chadd Academy
- wat is de de wortel van 9 tot de macht 3X
- Hoeveel is de wortel van drie met de macht van 3?
- De derdemachtswortel van een geheel getal
- Wortels – Theorie wiskunde
See more: toplist.prairiehousefreeman.com/vtm-nieuws
