Top 21 자계 의 세기 공식 Top Answer Update

You are looking for information, articles, knowledge about the topic nail salons open on sunday near me 자계 의 세기 공식 on Google, you do not find the information you need! Here are the best content compiled and compiled by the toplist.prairiehousefreeman.com team, along with other related topics such as: 자계 의 세기 공식 자기장의 세기, 자계의 세기 전류밀도, 도체 내부 자계, 자계 H, 자계 단위, 자속밀도 공식, 환상솔레노이드, 솔레노이드 자속밀도

기호로는 H로 나타내며, 단위는 A/m가 된다. B = μ H \mathbf{B} = \mu \mathbf{H} B=μH라는 관계가 성립한다. (단, μ는 매질의 투자율, B는 자기장이다.)

30 전류에 의한 자계의 세기01

[Lv1] 7장. 정자계 ① 자극의세기와 자계, 자기력선 및 자속과 자속밀도 :: 공부하는 피카츄

Article author: gongkachu12.tistory.com
Reviews from users: 19653 Ratings
Top rated: 4.9
Lowest rated: 1
Summary of article content: Articles about [Lv1] 7장. 정자계 ① 자극의세기와 자계, 자기력선 및 자속과 자속밀도 :: 공부하는 피카츄 자계(H). 쿨롱의 법칙 힘의 공식에서. 두 자극의 세기(m) 중에 하나를 1[Wb]로. 고정했을 때를 자계의 세기(H)라고 정의합니다. …
Most searched keywords: Whether you are looking for [Lv1] 7장. 정자계 ① 자극의세기와 자계, 자기력선 및 자속과 자속밀도 :: 공부하는 피카츄 자계(H). 쿨롱의 법칙 힘의 공식에서. 두 자극의 세기(m) 중에 하나를 1[Wb]로. 고정했을 때를 자계의 세기(H)라고 정의합니다. 안녕하세요! 드디어 전기자기학의 전기를 마치고 자기 파트로 넘어왔습니다 자기 파트의 첫 챕터가 ‘정자계’ 인데요 2장의 ‘정전계’ 에서 ‘전’ → ‘자’로 바뀐 것뿐이라고 해도 과언이 아닐만큼 내용 흐름이 유사..
Table of Contents:

인기포스트 MORE POST

TAG

[Lv1] 7장. 정자계 ① 자극의세기와 자계, 자기력선 및 자속과 자속밀도

안녕하세요!

드디어 전기자기학의 전기를 마치고

자기 파트로 넘어왔습니다

자기 파트의 첫 챕터가

‘정자계’ 인데요

2장의 ‘정전계’ 에서

‘전’ → ‘자’로 바뀐 것뿐이라고

해도 과언이 아닐만큼

내용 흐름이 유사합니다

전기쪽에서 썼던 용어와 기호를

자기쪽에 맞게 바꿔주기만 하면

되기 때문에

2장의 정전계를 잘 알고 있는 것이

중요하겠네요!

* 정자계, 자하, 자극의세기

정자계는 ‘정지해 있는 자하들의 공간’

이라고 이해하시면 됩니다

이 때 자하란 자기적 성질을 가진 기본입자

입니다

자하량은 m으로 나타내고

단위는 [Wb] (웨버) 라고 합니다

보통 자기는 자석의 형태로 다룹니다

한쪽끝을 N극 다른쪽끝을 S극이라고 합니다

자석 양극단의 세기인 자극의세기가

자하량에 의해 결정되므로

자하량과 자극의세기는 같은 것으로 봅니다

(자하량보다 자극의세기라는 말이

문제에 더 많이 나옵니다)

* 쿨롱의 법칙

자석의 같은 극끼리는 반발력이 작용하고

서로 다른 극끼리는 흡인력이 작용합니다

이 힘의 세기를 계산한 법칙이

쿨롱의 법칙입니다

( 쿨롱의 법칙은 전기와 자기쪽에서

모두 쓰는 법칙입니다.

식의 모양이 조금 다르지만 유사합니다 )

$$F=\frac{1}{4πμ_0}\frac{m_1 m_2}{r^2}=6.33×10^4×\frac{m_1 m_2}{r^2} [N]$$

m은 자하량 또는 자극의세기[Wb]
r은 거리[m]입니다

거리 제곱에 반비례하고

자하량의 곱에 비례합니다

* 투자율

$μ$라는 기호가 처음 나오는데요

투자율이라는 용어입니다

전계에서의 유전율(ε)과

대응시킬 수 있는데요

투자율이라는 말에서

‘자하가 잘 투과되는 정도’ 라는 의미로

생각하시면 됩니다

$ε=ε_0 ε_s$로 표현하듯이

$$μ=μ_0 μ_s$$

로 표현합니다

이 때 $μ_0$는 진공,공기에서의 투자율로

$$μ_0=4π×10^{-7}$$

입니다

$μ_s$는 비투자율로 매질마다 다르며

공기,진공에서의 몇 배인지를 나타냅니다

진공,공기에서는 $μ_s=1$ 입니다

위의 쿨롱의 법칙은

진공(공기)에서의 힘을 다룬 것으로

$\frac{1}{4πμ_0}$를 계산하면 $6.33×10^4$이 됩니다

$6.33×10^4$이라는 숫자를 기억하면

문제에서 틀린 것 찾을 때 도움이 됩니다

$6.33×10^{-4}$이라고 하면 틀린 것입니다

만약 진공이 아니라면

$μ_0$가 아닌 $μ$값을 공식에 대입해야 합니다

즉 $μ_0 μ_s$를 대입해야 하는 것입니다

* 자계(H)

쿨롱의 법칙 힘의 공식에서

두 자극의 세기(m) 중에 하나를 1[Wb]로

고정했을 때를 자계의 세기(H)라고 정의합니다

$$H=\frac{1}{4πμ_0}\frac{m}{r^2}=6.33×10^4×\frac{m}{r^2} [AT/m]$$

단위 [AT/m]에서 AT는 암페어턴이라고 읽는데

A는 암페어로서 전류와 관계된 단위임을 나타냅니다

자계와 전류와의 관계를 8장에서 자세히 다룰 예정입니다

T는 몇번을 감았는지를 나타내는 용어로

이것도 나중에 8장에서 다룹니다

우선 [AT/m] 이라는 단위를 눈에 익혀둡시다

F에서는 $m_1$과 $m_2$로 m이 2개인데

H의 공식에는 m이 하나입니다

즉 m이 하나 나눠진 형태로 볼 수 있습니다

따라서 힘 F와 자계 H 사이에는

$$F=mH$$

의 관계가 성립합니다

(전계에서 $F=QE$ 식에 대응)

문제에서 ‘자극의 세기(m)’와 ‘힘’이라는 말이 나오면

$F=mH$ 식을 적용하면 됩니다

* 자기력선

전계의 전기력선과 대응하는 개념으로

자석의 자극에 의한 힘, 자계의 세기를

가상의 선으로 가시화시켜 나타낸 선입니다

전기력선과 조금 대비되는 것은

자석 주위에 철가루를 뿌렸을 때

철가루가 배열되는 형태를 통해

자기력선의 특징을 눈으로

볼 수 있다는 점입니다

전기력선과 마찬가지로

자기력선도 여러가지 특징이 있지만

우선은 자기력선이

N극에서 나와서 S극으로 들어간다는 것을

알아둡시다!

* 자속과 자속밀도

자기력선의 묶음을 자속이라고 합니다

자기력선의 수가 매우 많아서

해석하기 복잡하므로

여러개를 한묶음으로 해석하는 것입니다

자속(Φ)은 자극의세기(m)와 같습니다

$Φ=m [Wb]$ 입니다 (단위도 같습니다)

자속밀도(B)는 단위면적당 자속을 말합니다

$$B=\frac{Φ}{S} [Wb/m^2]$$

입니다 (S는 면적입니다)

따라서 $Φ=BS$ 입니다

$Φ=m$과 같고

공간에서 자기력선은 구의 형태로

퍼져나가므로 면적(S)에

구의 면적인 $4πr^2$ 을 대입하면

$$B=\frac{m}{4πr^2} [Wb/m^2]$$

이 됩니다

이 때 아까 다룬 H의 식에서 $μ_0$를 곱하면

$$\frac{m}{4πμ_0 r^2}×μ_0 = \frac{m}{4πr^2} = B$$

즉

$$B=μ_0 H$$

의 관계가 성립합니다

공기나 진공중이 아니라면

$$B=μH = μ_0 μ_s H $$

가 됩니다

또한,

$Φ=BS$ 이므로

$$Φ = BS = μHS = μ_0 μ_s HS $$

까지 연결이 됩니다

$Φ=BS$와 $B=μH$ 식을 잘 숙지하고

문제에 따라 서로 잘 연결해서

사용할 수 있습니다

문제 풀어보겠습니다!

1

2

1

자극이라는 말과 힘이라는 말이 나오면

$F=mH$ 라는 식을 떠올리면 됩니다

문제에 주어진 것을 모두 기호로

써보는 것도 공식을 떠올리는데

도움이 되는데요

묻는게 힘인데 힘은 F

자계 $10[AT/m]$은 H이고

$5×10^{-3}$의 자극은 m이므로

F=mH를 떠올리기가 쉽습니다

$10$과 $5×10^{-3}$를 곱하면 답이네요

$5×10^{-2}$

답은 ①번입니다

2

문제에서 주어진 것을 기호화 해봅시다

단면적 $S$

자속 $Φ$

자계 $H$

비투자율 $μ_s$

저 기호들을 조합해보면

$$Φ = BS = μHS = μ_0 μ_s HS $$

식을 떠올릴 수 있습니다

비투자율 $μ_s$를 물었기 때문에

$Φ= μ_0 μ_s HS$를 변형하여

주어진 값을 대입하면

$$μ_s =\frac{Φ}{ μ_0 HS}=\frac{6×10^{-4}}{4π×10^{-7} × 2800 × (4×10^{-4})}$$

$$≒ 426$$

답은 ④번입니다

7장부터 다루는 자기 파트는

문제에서 특정 키워드가 나오면

이 공식을 쓰면 된다고 말하기

까다로운 부분들이 있습니다

자기 파트를 모두 공부해보신분은 알고 계시겠지만

자속이나 자계, 투자율이 들어가는

공식이 많기 때문입니다

문제를 보고 바로 적용할 공식이

떠오르면 제일 좋고 잘 모르겠다면

문제에서 주어진 것들을 모두 기호로 써보고

그로부터 알고 있는 공식을 떠올리는 식으로

접근하는 연습이 필요합니다

많은 문제를 풀어보고

연습해야하는 부분이고

저 또한 더 쉽게 구분할 수 있는

방법이 있을지 계속 공부하고

연구해보겠습니다!

< 요약 >

정자계 첫 번째 포스팅 마무리하겠습니다

2장에서 공부했던 내용 전개와

유사하기 때문에 2장을 잘 기억하시면

이해하기에 조금 수월할 수 있을 것 같네요

7장 두번째 포스팅으로

이어가겠습니다

감사합니다!

전기자기학 7장 – 정자계 + 자극의세기와 자계 + 자기력선 및 자속밀도

안녕하세요, 오늘 다룰 내용은 자극의세기와 자계, 자기력선 및 자속과 자속밀도에 대해서 나름대로 정리해서 설명 드리도록 하겠습니다. 쉬운 이해를 돕기 위해서 그림이나 공식도 추가하여 설명 드리도록 하겠습니다.

1. 정자계

: 정전계에서 “전” 를 “자” 짜로만 고치고 바라 보시면 더 공식 외우기도 쉽고, 이해하기도 쉬우 실겁니다. 하지만 전제는 정전계에 대해서 나름대로 이해가 되셨다는 전제입니다!

▼ 정자계는 ‘정지해 있는 자하들의 공간’ 이라고 이해하시면 됩니다. 자하란 자기적 성질을 가진 기본입자입니다. (약간 전하를 설명할 때 같은 패턴으로 설명하신 거 눈치 채셨죠?!) 자하량은 m으로 나타내고 단위는 [Wb] (웨버) 라고 합니다.

보통 자기는 자석의 형태로 다루는데요, 한쪽끝을 N극 다른쪽끝을 S극이라고 합니다. 자석 양극단의 세기인 자극의세기가 자하량에 의해 결정되므로 자하량과 자극의세기는 같은 것으로 봅니다. 전계의 세기도 전하량에 의해 결정되는 거와 비슷하다고 생각하시면 됩니다.

자료 참조 : https://gongkachu12.tistory.com

2. 쿨롱의 법칙 In 정자계

: 정자계에서의 쿨롱의 법칙을 설명을 드릴려고 합니다. 자석의 같은 극끼리는 반발력이 작용하고 서로 다른 극끼리는 흡인력이 작용합니다. 이 힘의 세기를 계산한 법칙이 쿨롱의 법칙입니다.

▼ 정전계, 정자계 두 쪽 모두 쿨롱의 법칙을 사용하게 됩니다.

쿨롱의-법칙

(m은 자하량 또는 자극의세기[Wb], r은 거리[m])

쿨롱의-법칙

(거리 제곱에 반비례, 자하량의 곱에 비례)

자료 참조 : https://gongkachu12.tistory.com

3. 투자율

: 2번 쿨롱의 법칙에서 보신 μ에 대해서 설명 드리도록 하겠습니다. 투자율을 기호로 μ 라고 사용합니다. 전계에서의 유전율(ε)과 대응해서 이해하시면 더 도움이 되실 겁니다.

▼ 투자율이라는 의미는 ‘자하가 잘 투과되는 정도’ 라는 의미로 이해하시면 됩니다.

투자율

μ0는 진공,공기에서의 투자율로

투자율

▼ μs는 비투자율로 매질마다 다르며 공기,진공에서의 몇 배인지를 나타냅니다 (진공,공기에서는μs = 1 입니다.)

이어서 자계(H)에 대해서 설명 드리도록 하겠습니다. 쿨롱의 법칙 힘의 공식에서 두 자극의 세기(m) 중에 하나를 1[Wb]로 고정했을 때를 자계의 세기(H)라고 정의합니다. 전계의 세기도, 두 전하 중에 하나를 “1[C]” 로 고정했을 때의 세기를 나타내는 것을 이해하시고 있다면, 이 정의 내용은 이해하기 쉬우실 겁니다.

▼ A는 암페어로서 전류와 관계된 단위임을 나타내고, – T는 몇번을 감았는지를 나타내는 용어입니다. 참조 하세요!

자계

(단위 [AT/m]에서 AT는 암페어턴)

▼ 추가적으로 힘 F와 자계 H 사이의 식을 계산해보면 아래와 같은 공식을 유도 해 볼 수 잇습니다.

전계-자계

힘-자계

자료 참조 : https://gongkachu12.tistory.com

다음으로는 자기력선에 대해서 설명 드리도록 하겠습니다. 전계의 전기력선과 대응하는 개념으로 자석의 자극에 의한 힘, 자계의 세기를 가상의 선으로 가시화시켜 나타낸 선입니다. 전기력선과 조금 대비되는 것은 자석 주위에 철가루를 뿌렸을 때 철가루가 배열되는 형태를 통해 자기력선의 특징을 눈으로 볼 수 있다는 점입니다.

▼ 가장 큰 차이점은 발산과 회전입니다.- 전기력선은 발산만 할뿐 다시 돌아오는 회전은 하지 않습니다.

하지만, 자석에 철가구를 뿌리면, 자기력선이 N극에서 나와서 S극으로 들어가는 형태를 보실 수 있습니다. 즉, 자기력선은 발산을 하지 않고, 회전을 합니다.

자기력선

자료 참조 : https://gongkachu12.tistory.com

마지막으로 자속과 자속밀도에 대해서 설명 드리도록 하겠습니다. 전기력선의 묶음을 전속이라고 했던 것 처럼, 자기력선의 묶음을 자속이라고 합니다. 자기력선의 수가 매우 많아서 해석하기 복잡하므로 여러개를 한묶음으로 해석하는 것입니다. (전속을 설명할때와 똑같은 내용입니다.)

자속(Φ) = 자극의세기(m) (단위도 Wb로 동일합니다.)

자속

▼ 자속밀도(B)는 이런 자속을 면적으로 나눈 값으로, 다른 말로, 단위면적당 자속을 말합니다.- 일단 면적은 구의 면적을 가지고 설명 드리도록 하겠습니다. (S = 4πr2)

자속-밀도

자속과 자속밀도가 자계와 투자율과 어떤 관계를 가지게 되는지에 대한 공식을 나열해 보면Φ=BS 인 상태에서, Φ=m과 같고, 공간에서 자기력선은 구의 형태로 퍼져나가므로면적(S)에 구의 면적인 4πr2 을 대입하고 H의 식에서 μ0를 곱하면

자속-밀도

▼ 그러면 자속, 자속밀도 그리고 자계와 관계를 다시 종합하면 아래와 같습니다.

자속-밀도

자료 참조 : https://gongkachu12.tistory.com

요점-정리

이상입니다. 전계에 대해서 미리 공부를 해서 그런지, 약간 응용해서 공식을 생각하니까, 처음에 전계 공식을 이해했을 대보다는 더 수월하게 이해를 했던 거 같습니다. 용어 자체가 헷갈리는 건지 아니면 이론 자체가 정리가 안된 건지는 모르겠지만, 간혹 혼돈이 되서, 이게 이건지를 혼자서 되씹는 과정이 아직까지는 필요한 상태인 거 같습니다. 오늘도 공부하시느라 수고 하셨고, 계속 같이 공부해서, 같이 성장하시죠! 감사합니다.
[참조 자료 출처 : https://gongkachu12.tistory.com] [저작권이나, 권리를 침해한 사항이 있으면 언제든지 Comment 부탁 드립니다. 검토 후 수정 및 삭제 조치 하도록 하겠습니다. 그리고, 기재되는 내용은 개인적으로 습득한 내용이므로, 혹 오류가 발생할 수 있을 가능성이 있으므로, 기재된 내용은 참조용으로만 봐주시길 바랍니다. 게시물에, 오류가 있을때도, Comment 달아 주시면, 검증 결과를 통해, 수정하도록 하겠습니다.]
다른 사람들도 좋아하는 글

자기력(F)과 자기장의 세기(B)

■ 전기력(F)과 전기장의 세기(E)

■ 자기력(F)과 자기장의 세기(B)

전기력은 두 전하의 거리 제곱(r^2)에 반비례하지만, 자기력은 두 전류의 거리(r)에 반비례합니다.

■ 비오-사바르 법칙(Biot-Savart Law)

<그림출처 : Biot–Savart law - 위키백과>

(투자율 μ o = 4π x 10-7 H/m)

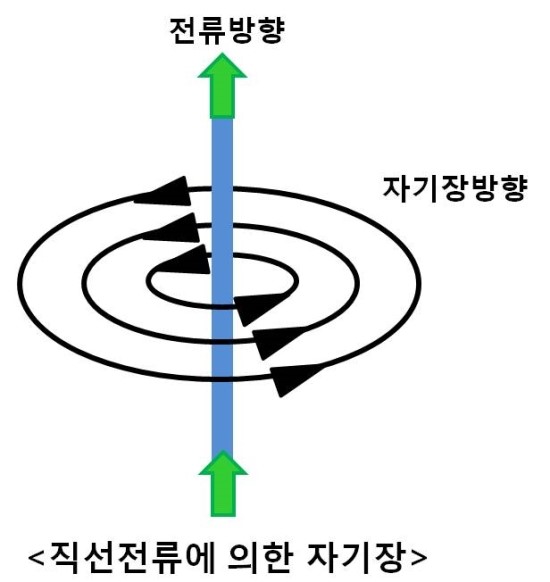
비오-사바르의 법칙은 전자기학에서 주어진 전류가 생성하는(만드는) 자기장(B)이 전류에 대해 수직이고, 전류에서의 거리의 역제곱(1/r^2)에 비례한다는 물리 법칙입니다.(= 거리 제곱에 반비례). 또한 자기장이 전류의 세기, 방향, 길이에 연관이 있음을 알려줍니다.

따라서 거리(r)와 비교하면, 전기력(F)은 두 전하(q)의 거리 제곱(r^2)에 반비례, 자기력(F)은 두 전류(i)의 거리(r)에 반비례, 이에 따른 전기장(E)의 세기와 자기장(B)의 세기도 마찬가지로 각각 r^2과 r에 반비례, 다만 비오-사바르의 법칙에서 전류(i)가 생성하는 수직성분의 자기장(B)의 세기는 전류로부터의 거리 제곱(r^2)에 반비례. 직선 와이어의 경우 앙페르의 법칙 및 오른나사법칙과 같아짐.

■ 진공의 유전율과 투자율

■ 자기장의 세기(B,자기선속밀도,자속밀도) 정리

■ 자기장의 세기(B,자기선속밀도,자속밀도)와 자계 세기(H)

■ 자기장의 세기(B,자기선속밀도)와 자기력선속(Φ,자속)

자기력선속(magnetic flux,자속)은 자기장의 세기(B,자기밀도)에 면적(S)을 곱한 값입니다.

So you have finished reading the 자계 의 세기 공식 topic article, if you find this article useful, please share it. Thank you very much. See more: 자기장의 세기, 자계의 세기 전류밀도, 도체 내부 자계, 자계 H, 자계 단위, 자속밀도 공식, 환상솔레노이드, 솔레노이드 자속밀도

Top 21 자계 의 세기 공식 Top Answer Update

[Lv1] 7장. 정자계 ① 자극의세기와 자계, 자기력선 및 자속과 자속밀도 :: 공부하는 피카츄

전기자기학 7장 – 정자계 + 자극의세기와 자계 + 자기력선 및 자속밀도

자기력(F)과 자기장의 세기(B) : 네이버 블로그

자계 의 세기 공식

자계 의 세기 공식

자기장과 자계

Top 45 자계 의 세기 공식 The 198 New Answer

[Lv1] 7장. 정자계 ① 자극의세기와 자계, 자기력선 및 자속과 자속밀도

전기자기학 7장 – 정자계 + 자극의세기와 자계 + 자기력선 및 자속밀도

자기력(F)과 자기장의 세기(B)

Leave a Comment Cancel reply