Hoe Deel Je Breuken: Stapsgewijze Uitleg Voor Beginners
How To Divide A Fraction By A Fraction | Math With Mr. J
Keywords searched by users: hoe deel je breuken ezelsbruggetje breuken delen, breuken vermenigvuldigen, hoe deel je breuken door breuken, hoe deel je een breuk door een heel getal, breuken delen groep 8, breuken delen voorbeeld, wat is de helft van 1/4, breuken delen oefeningen
Wat zijn breuken?
Breuken zijn een fundamenteel concept binnen de wiskunde. Ze stellen een deel van een geheel voor. Een breuk bestaat uit een teller en een noemer, gescheiden door een streepje. De teller geeft aan hoeveel delen we hebben, terwijl de noemer aangeeft in hoeveel gelijke delen het geheel is verdeeld.
Breuken worden over het algemeen geschreven als een breukstreep tussen twee getallen, bijvoorbeeld 3/4 of 5/8. Hierbij is de teller kleiner dan de noemer, wat betekent dat we een deel van een geheel hebben.
Het begrijpen van breuken is cruciaal voor verschillende wiskundige concepten en toepassingen, zoals het oplossen van vergelijkingen, werken met decimalen en het meten van hoeveelheden.
Begrijpen hoe breuken werken
Om breuken correct te kunnen delen, is het belangrijk om een goed begrip te hebben van hoe breuken werken. Hier zijn enkele basisprincipes die je moet begrijpen:
1. De noemer geeft het aantal gelijke delen aan waarin het geheel is verdeeld.
2. De teller geeft aan hoeveel van die delen we hebben.
3. De waarde van de breuk wordt bepaald door de verhouding tussen de teller en de noemer. Een breuk met een kleine teller en een grote noemer stelt een klein deel voor, terwijl een breuk met een grote teller en een kleine noemer een groot deel vertegenwoordigt.
4. Breuken kunnen worden vereenvoudigd door de teller en de noemer met hetzelfde getal te delen.
Stapsgewijze uitleg van breuken delen
Het delen van breuken kan intimiderend lijken, maar met de juiste stappen en begeleiding wordt het gemakkelijker. Hier is een stapsgewijze uitleg van hoe je breuken kunt delen:
Stap 1: Keer de tweede breuk om
Om twee breuken met elkaar te delen, keer je de tweede breuk om. Dit betekent dat je de teller en de noemer van positie wisselt. Bijvoorbeeld, als je 3/4 wilt delen door 1/2, keer je 1/2 om en wordt het 2/1.
Stap 2: Vermenigvuldig de eerste breuk met de omgekeerde van de tweede breuk
Vermenigvuldig vervolgens de eerste breuk met de omgekeerde van de tweede breuk. Dit doe je door de tellers met elkaar te vermenigvuldigen en de noemers met elkaar te vermenigvuldigen. In ons voorbeeld wordt 3/4 vermenigvuldigd met 2/1, wat resulteert in (3 * 2) / (4 * 1) = 6/4.
Stap 3: Vereenvoudig de verkregen breuk
Om de breuk te vereenvoudigen, deel je de teller en de noemer door hun grootste gemene deler. In dit geval is de grootste gemene deler van 6 en 4 gelijk aan 2. Dus, 6/4 gedeeld door 2/2 wordt (6/4) / (2/2) = 3/2.
Bij het delen van breuken is het belangrijk om te onthouden dat je altijd moet zorgen voor een gemeenschappelijke noemer voordat je begint met delen. Dit helpt om de berekeningen eenvoudiger te maken en vereenvoudigde breuken te verkrijgen.
Voorbeeldproblemen oplossen
Om het delen van breuken beter te begrijpen, laten we een aantal voorbeeldproblemen oplossen:
Voorbeeld 1: 2/3 ÷ 4/5
1. Omkeren van de tweede breuk: 4/5 wordt 5/4.
2. Vermenigvuldigen van de eerste breuk met de omgekeerde van de tweede breuk: (2/3) * (5/4) = (2 * 5) / (3 * 4) = 10/12.
3. Vereenvoudigen van de breuk: 10/12 wordt 5/6.
Voorbeeld 2: 7/8 ÷ 1/2
1. Omkeren van de tweede breuk: 1/2 wordt 2/1.
2. Vermenigvuldigen van de eerste breuk met de omgekeerde van de tweede breuk: (7/8) * (2/1) = (7 * 2) / (8 * 1) = 14/8.
3. Vereenvoudigen van de breuk: 14/8 wordt 7/4.
Let op: Als de resultaatbreuk een oneven noemer heeft, kan het nuttig zijn om deze als een gemengd getal te schrijven. Bijvoorbeeld, 7/4 kan worden geschreven als 1 3/4.
Oefeningen en praktische toepassingen van breuken delen
Om je vaardigheden in het delen van breuken te verbeteren, kun je oefeningen doen en praktische toepassingen verkennen. Hier zijn enkele ideeën om aan de slag te gaan:
1. Oefen met wiskunde-oefeningen: Gebruik online bronnen zoals Slimleren en Khan Academy om oefeningen te vinden die gericht zijn op het delen van breuken. Test jezelf op verschillende niveaus van moeilijkheid om je begrip te vergroten.
2. Bakken en koken: Recepten vereisen vaak het delen van ingrediënten. Gebruik je kennis van breuken om recepten aan te passen aan het aantal porties dat je wilt maken.
3. Knutselprojecten: Probeert u een kunstwerk te maken dat is verdeeld in gelijke delen? Gebruik breuken om de verhoudingen te berekenen en de delen gelijkmatig te verdelen.
4. Meetverhoudingen: Als je bijvoorbeeld een verfproject hebt, gebruik je breuken om de verhouding tussen de verf en de verdunner te berekenen.
Door praktische toepassingen van breuken te verkennen, kun je de concepten beter begrijpen en zien hoe ze in het dagelijks leven van toepassing zijn.
Speciale manieren om breuken te delen
Naast de standaardmethode om breuken te delen, zijn er enkele speciale scenario’s die een andere aanpak vereisen. Hier zijn twee van die scenario’s:
1. Breuken delen door breuken: Om twee breuken door elkaar te delen, keer je de tweede breuk om en vermenigvuldig je de eerste breuk met de omgekeerde van de tweede breuk. Bijvoorbeeld, 3/4 ÷ 2/3 wordt (3/4) * (3/2) = 9/8.
2. Een breuk delen door een heel getal: Om een breuk te delen door een heel getal, vermenigvuldig je de breuk met het omgekeerde van het hele getal. Bijvoorbeeld, 3/4 ÷ 2 wordt (3/4) * (1/2) = 3/8.
Het is belangrijk om te onthouden dat bij het delen van breuken de volgorde van de bewerkingen cruciaal is. Zorg ervoor dat je de juiste stappen volgt en de breuken correct omkeert voordat je begint te vermenigvuldigen.
Belang van het vereenvoudigen van breuken
Bij het delen van breuken is het belangrijk om de verkregen breuk te vereenvoudigen. Dit betekent dat je de teller en de noemer van de breuk deelt door hun grootste gemene deler. Het vereenvoudigen van breuken helpt om ze in de eenvoudigst mogelijke vorm te presenteren en maakt verdere berekeningen gemakkelijker.
Als een breuk niet volledig is vereenvoudigd, kan dit leiden tot verwarring en onjuiste resultaten bij verdere bewerkingen of toepassingen.
Ezelsbruggetje breuken delen
Om breuken te delen, volg je de stappen: “Keer, keer en vermenigvuldig!” Keer de tweede breuk om, vermenigvuldig de eerste breuk met de omgekeerde van de tweede breuk.
Breuken vermenigvuldigen
Om breuken te vermenigvuldigen, vermenigvuldig je de tellers met elkaar en de noemers met elkaar. Het resultaat is een nieuwe breuk.
Hoe deel je breuken door breuken
Om breuken door breuken te delen, keert je de tweede breuk om en vermenigvuldig je de eerste breuk met de omgekeerde van de tweede breuk.
Hoe deel je een breuk door een heel getal
Om een breuk door een heel getal te delen, vermenigvuldig je de breuk met het omgekeerde van het hele getal.
Breuken delen groep 8
In groep 8 worden kinderen meestal geïntroduceerd aan het delen van breuken. Ze leren de basisstappen en oefenen met eenvoudige voorbeelden om hun begrip te vergroten.
Breuken delen voorbeeld
Een voorbeeld van het delen van breuken is het delen van 3/4 door 1/2. In dit geval keer je 1/2 om en vermenigvuldig je 3/4 met 2/1, wat resulteert in 6/4. Deze breuk kan verder worden vereenvoudigd tot 3/2.
Wat is de helft van 1/4
De helft van 1/4 is 1/8. Dit betekent dat 1/4 kan worden verdeeld in 2 gelijke delen, en 1/8 vertegenwoordigt één van die gelijke delen.
Breuken delen oefeningen
Om je vaardigheden in het delen van breuken te oefenen, kun je verschillende oefeningen doen. Gebruik online oefenplatforms zoals Slimleren en Khan Academy om specifieke oefeningen te vinden en je begrip te vergroten.
Het delen van breuken is een belangrijke vaardigheid binnen de wiskunde en heeft talloze toepassingen in het dagelijks leven. Door de stappen te begrijpen en te oefenen met verschillende voorbeelden, kun je jezelf vertrouwd maken met het delen van breuken en je wiskundige vaardigheden vergroten.
Categories: Verzamelen 73 Hoe Deel Je Breuken

Twee breuken op elkaar delen is hetzelfde als de eerste breuk met het omgekeerde van de tweede breuk te vermenigvuldigen. De eerste stap is daarom om het omgekeerde van de tweede breuk te bepalen (waarbij de teller en de noemer van plaats gewisseld zijn). Daarna vermenigvuldig je de twee tellers.Om breuken te vermenigvuldigen, vermenigvuldig je de tellers (de bovenste cijfers/getallen) met elkaar en vermenigvuldig je de noemers (de onderste cijfers/getallen) met elkaar.Hoe gebruik je breuken? Bij een breuk bereken je eerst alles boven de deelstreep, vervolgens alles onder de deelstreep en dáárna deel je het pas door elkaar. Als geheugensteuntje kun je doen alsof alles zowel boven als onder de deelstreep tussen haakjes staat.
- Een getal delen door een breuk is hetzelfde als het getal vermenigvuldigen met het omgekeerde van de breuk.
- Een breuk delen door een breuk is hetzelfde als de breuk vermenigvuldigen met het omgekeerde van de breuk.
- Stap 1. Delen door een breuk is vermenigvuldigen met het omgekeerde.
- Stap 2. Vermenigvuldig de tellers en noemers met elkaar.
- Stap 3. Vereenvoudig indien mogelijk.
Hoe Deel Je Breuken Voorbeeld?
Hoe Deel Je Ongelijke Breuken?
Stap 1: Om een breuk te delen, vermenigvuldig je deze met het omgekeerde van de andere breuk.
Stap 2: Vermenigvuldig de tellers en noemers van de twee breuken met elkaar.
Stap 3: Als je kunt, vereenvoudig dan de resulterende breuk.
Op deze manier kun je ongelijke breuken delen en de juiste resultaten verkrijgen.
Hoe Doe Je 2 Breuken Keer Elkaar?
Hoe Doe Je Breuken Uitrekenen?
Details 33 hoe deel je breuken

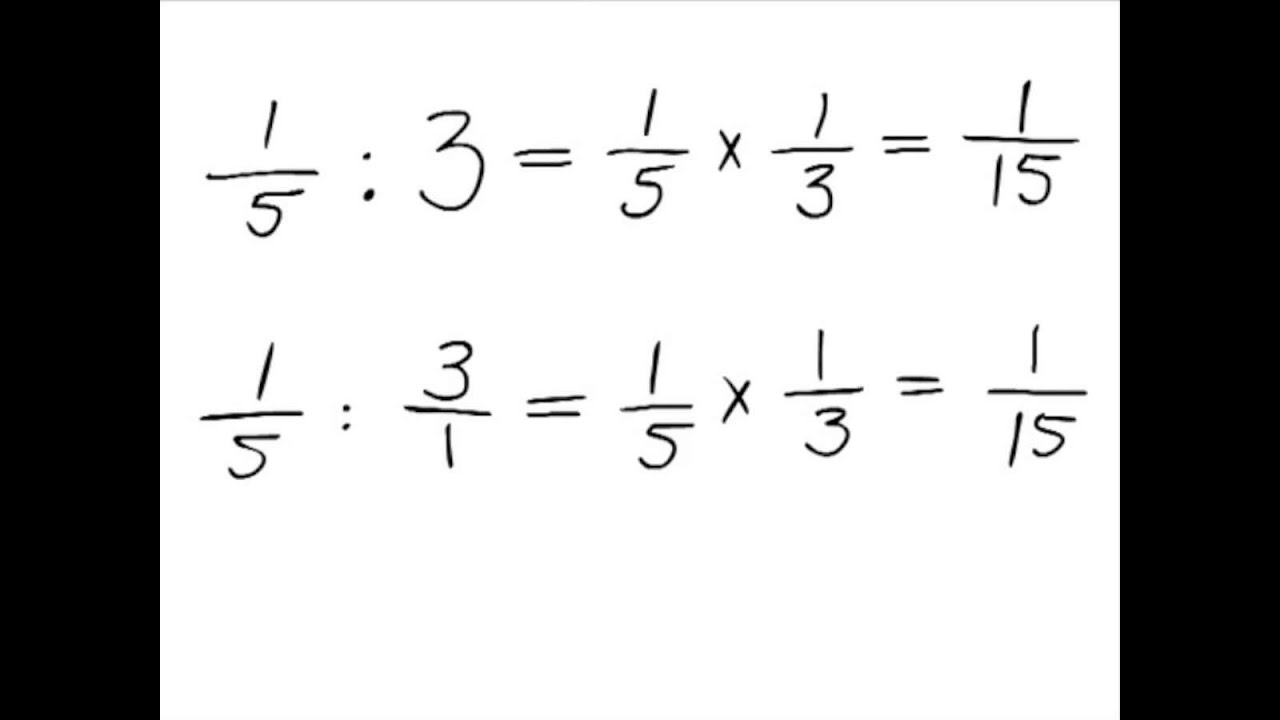





See more here: toplist.prairiehousefreeman.com
Learn more about the topic hoe deel je breuken.
- Breuken delen – Slimleren
- Breuken delen: 3/5 ÷ 1/2 (video) – Khan Academy
- Ongelijknamige breuken door elkaar delen (open) – Slimleren
- heb je een speciale manier om breuken keer elkaar te doen zoals 4 …
- Rekenen met Breuken: Hoe Doe Je Dat? (Uitleg + Voorbeelden)
- Eerste hulp bij breuken – vermenigvuldigen, delen, en meer
See more: toplist.prairiehousefreeman.com/vtm-nieuws
