You are looking for information, articles, knowledge about the topic nail salons open on sunday near me exercice suite arithmétique pdf on Google, you do not find the information you need! Here are the best content compiled and compiled by the toplist.prairiehousefreeman.com team, along with other related topics such as: exercice suite arithmétique pdf suites arithmétiques et géométriques exercices corrigés pdf, exercices corrigés suites arithmétiques pdf, exercice suite arithmétique corrigé, suite arithmétique exercice corrigé bac pro pdf, exercices corrigés suites terminale es pdf, exercices suites arithmétiques et géométriques 1ère, suite arithmétique exercice corrigé 1ere, somme suite arithmétique exercice corrigé
Comment calculer une suite arithmétique exemple ?
Exemple : Considérons une suite numérique (un) où la différence entre un terme et son précédent reste constante et égale à 5. Si le premier terme est égal à 3, les premiers termes successifs sont : u0 = 3, u1 = 8, u2 = 13, u3 = 18. Une telle suite est appelée une suite arithmétique de raison 5 et de premier terme 3.
Comment expliquer une suite arithmétique ?
Si la suite est une suite arithmétique, le nombre réel r s’appelle la raison de cette suite. Autrement dit, une suite est arithmétique si et seulement si chaque terme s’obtient en ajoutant au terme précédent un nombre réel r, toujours le même.
Comment calculer la raison suite arithmétique ?
La raison d’une suite arithmétique, dont le premier terme u1 est égal à a , est donnée par la formule : r=un−an−1 r = u n – a n – 1 . Ce résultat signifie que, pour déterminer la raison, il faut retrancher au dernier terme le premier, puis diviser le résultat obtenu par le nombre de termes diminué de 1.
Comment montrer une suite ni arithmétique ni géométrique ?
Pour montrer qu’une suite (Un) n’est pas arithmétique, il suffit de calculer les 3 premiers termes U0, U1 et U2 (ou parfois les 4 ou 5 premiers, si les 3 premiers ne suffisent pas) et de constater que U_2 – U_1 \ne U_1 – U_0.
Comment trouver R ?
Plus la valeur R est élevée, meilleur est le système d’isolation. Pour calculer la valeur R d’une structure qui est composée de plusieurs couches, on additionnera les valeurs R. Formule : Valeur R = épaisseur isolation / valeur λ.
Comment calculer u50 ?
De plus, u50 = u0 +50r, soit u0 = u50 −50r = 406−50×8 = 6 2.
Quels sont les éléments caractéristiques d’une suite arithmétique ?
Par définition, une suite arithmétique est une suite où chacun des termes est égal à la somme du terme précédent et d’un nombre fixe. Par exemple, la suite. 3,5,7,9,… 3,5,7,9,…
Comment calculer la suite ?
On considère une suite (un) définie pour tout entier naturel n par un+1=f(un) où f est une fonction donnée. De plus, le premier terme u0 est également connu. Si l’exercice demande de calculer u1, on peut se servir de la relation un+1=f(un) en remplaçant n par 0. On obtient alors u0+1=f(u0), c’est à dire u1=f(u0).
C’est quoi le terme d’une suite ?
Définition : Une suite est une « succession » de nombres réels. Ces nombres réels sont les termes de la suite. Une suite (un) associe, à tout entier n, un nombre réel noté un et appelé le terme général de la suite. La notation un est la notation indicielle, n est appelé l’indice ou le rang.
Comment calculer la somme des termes d’une suite arithmétique ?
La somme de n termes consécutifs d’une suite arithmétique est égale à la demi-somme des premier et dernier termes, multipliée par le nombre de termes.
Comment calculer le nième terme d’une suite arithmétique ?
Le nième terme d’une suite arithmétique est égal à la somme du premier terme et du produit de la raison par (n-1). Le nième terme de la suite est donc donnée par la formule suivante : a+r(n−1) a + r ( n − 1 ) .
Comment trouver q ?
- Q=m⋅c⋅△T. …
- Un thermomètre indique que la température de l’eau d’un chaudron sur une plaque chauffante a augmenté de 10 ∘C 10 ∘ C .
Comment savoir si la suite est géométrique ?
Une suite $(u_{n})$ est géométrique si et seulement si pour tout entier naturel $n$, $u_{n+1}=a\times u_{n}$ où $a$ est un nombre indépendant de $n$. Pour démontrer qu’un suite est géométrique, on peut donc montrer qu’elle respecte bien la relation $u_{n+1}=a\times u_{n}$. Donc $(u_{n})$ est géométrique de raison $a$.
Comment calculer la somme d’une suite quelconque ?
La somme de termes consécutifs d’une suite arithmétique est égale au produit du nombre de termes par la demi-somme des termes extrêmes . Ex : Soit ( u n ) une suite arithmétique de raison r . Soit ( v n ) la suite arithmétique de raison 4 et de premier terme v 0 = 15 .
Quelle est la nature de la suite ?
La suite (un) est décroissante.
Comment calculer la suite ?
On considère une suite (un) définie pour tout entier naturel n par un+1=f(un) où f est une fonction donnée. De plus, le premier terme u0 est également connu. Si l’exercice demande de calculer u1, on peut se servir de la relation un+1=f(un) en remplaçant n par 0. On obtient alors u0+1=f(u0), c’est à dire u1=f(u0).
Comment calculer la somme d’une suite ?
La somme des termes d’une suite géométrique un, entre les indices p et n, est donnée par la formule suivante : up+up+1+… +un=up⋅1-qn-p+11-q, q est la raison de la suite.
Comment calculer u1 u2 u3 ?
Ici, dans les expressions obtenues, on aura u1 en fonction de u0 ; u2 en fonction de u1 ; u3 en fonction de u2… Comme u0 = 1, on a u0+1 = −3u0 +2 soit u1 = −3×1+2 = −1 u1+1 = −3u1 +2 soit u2 = −3×(−1)+2 = 5 u3 = −3u2 +2 = −3×5+2 = −13 u4 = −3u3 +2 = −3×(−13)+2 = 41 u5 = −3u4 +2 = −3×41+2 = −121. 2.
Comment calculer la somme des n premiers termes d’une suite arithmétique ?
Démonstration : somme des termes d’une suite arithmétique
(0 ⩽ p ⩽ n), on a : up + un−p = u0 + un. Soit Sn = u0 + u1 + u2 + … + un la somme des n + 1 premiers termes de la suite (un).
exercice suite arithmétique pdf
- Article author: s4f7287985a32ae60.jimcontent.com
- Reviews from users: 6596
Ratings
- Top rated: 3.5
- Lowest rated: 1
- Summary of article content: Articles about exercice suite arithmétique pdf (c’est-à-dire la somme des 50 premiers nombres pairs). Page 2. www.mathsenligne.com. SUITES ARITHMETIQUES. EXERCICES 2A. …
- Most searched keywords: Whether you are looking for exercice suite arithmétique pdf (c’est-à-dire la somme des 50 premiers nombres pairs). Page 2. www.mathsenligne.com. SUITES ARITHMETIQUES. EXERCICES 2A.
- Table of Contents:

exercice suite arithmétique pdf
- Article author: physique-et-maths.fr
- Reviews from users: 42166
Ratings
- Top rated: 3.3
- Lowest rated: 1
- Summary of article content: Articles about exercice suite arithmétique pdf Exercice 5 corrigé disponible. 1/4. Suites arithmétiques et géométriques – Exercices – Devoirs. Mathématiques Première générale – Année scolaire 2021/2022. …
- Most searched keywords: Whether you are looking for exercice suite arithmétique pdf Exercice 5 corrigé disponible. 1/4. Suites arithmétiques et géométriques – Exercices – Devoirs. Mathématiques Première générale – Année scolaire 2021/2022.
- Table of Contents:

exercice suite arithmétique pdf
- Article author: lycee.lagrave.free.fr
- Reviews from users: 4814
Ratings
- Top rated: 3.4
- Lowest rated: 1
- Summary of article content: Articles about exercice suite arithmétique pdf Est-ce une suite arithmétique ou géométrique ? Quelle est la raison de cette suite ? Exercice n°11. Les nombres suivants sont-ils en progression géométrique ? …
- Most searched keywords: Whether you are looking for exercice suite arithmétique pdf Est-ce une suite arithmétique ou géométrique ? Quelle est la raison de cette suite ? Exercice n°11. Les nombres suivants sont-ils en progression géométrique ?
- Table of Contents:

exercice suite arithmétique pdf
- Article author: leprofdemath.com
- Reviews from users: 26231
Ratings
- Top rated: 3.0
- Lowest rated: 1
- Summary of article content: Articles about exercice suite arithmétique pdf SUITES ARITHMÉTIQUES ET GÉOMÉTRIQUES. Fiche d’exercices. Première S. Exercice 1. Pour les questions suivantes, préciser si la suite ( )n u est arithmétique … …
- Most searched keywords: Whether you are looking for exercice suite arithmétique pdf SUITES ARITHMÉTIQUES ET GÉOMÉTRIQUES. Fiche d’exercices. Première S. Exercice 1. Pour les questions suivantes, préciser si la suite ( )n u est arithmétique …
- Table of Contents:

exercice suite arithmétique pdf
- Article author: www.maths-et-tiques.fr
- Reviews from users: 27680
Ratings
- Top rated: 3.1
- Lowest rated: 1
- Summary of article content: Articles about exercice suite arithmétique pdf Updating …
- Most searched keywords: Whether you are looking for exercice suite arithmétique pdf Updating
- Table of Contents:

Suites arithmetiques et géométriques – Cours maths 1ère – Educastream
- Article author: www.educastream.com
- Reviews from users: 24913
Ratings
- Top rated: 4.5
- Lowest rated: 1
- Summary of article content: Articles about Suites arithmetiques et géométriques – Cours maths 1ère – Educastream Updating …
- Most searched keywords: Whether you are looking for Suites arithmetiques et géométriques – Cours maths 1ère – Educastream Updating
- Table of Contents:
Suites arithmétiques
Suites géométriques
Sommaires
Raison du suite arithmétique
- Article author: les-suites.fr
- Reviews from users: 9290
Ratings
- Top rated: 4.8
- Lowest rated: 1
- Summary of article content: Articles about Raison du suite arithmétique Updating …
- Most searched keywords: Whether you are looking for Raison du suite arithmétique Updating Déterminer la raison du suite arithmétique.raison,suite
- Table of Contents:
Raison d’une suite arithmétique
Formule de la raison d’une suite arithmétique

Suites arithmétiques et suites géométriques – Assistance scolaire personnalisée et gratuite – ASP
- Article author: www.assistancescolaire.com
- Reviews from users: 32017
Ratings
- Top rated: 3.5
- Lowest rated: 1
- Summary of article content: Articles about Suites arithmétiques et suites géométriques – Assistance scolaire personnalisée et gratuite – ASP Updating …
- Most searched keywords: Whether you are looking for Suites arithmétiques et suites géométriques – Assistance scolaire personnalisée et gratuite – ASP Updating
- Table of Contents:

(PDF) Cours et exercices de mathématiques SUITES ARITHMETIQUES ET GEOMETRIQUES EXERCICES CORRIGES | ISMAIL ouaaziz – Academia.edu
- Article author: www.academia.edu
- Reviews from users: 4580
Ratings
- Top rated: 3.8
- Lowest rated: 1
- Summary of article content: Articles about (PDF) Cours et exercices de mathématiques SUITES ARITHMETIQUES ET GEOMETRIQUES EXERCICES CORRIGES | ISMAIL ouaaziz – Academia.edu Cours et exercices de mathématiques SUITES ARITHMETIQUES ET GEOMETRIQUES EXERCICES CORRIGES. …
- Most searched keywords: Whether you are looking for (PDF) Cours et exercices de mathématiques SUITES ARITHMETIQUES ET GEOMETRIQUES EXERCICES CORRIGES | ISMAIL ouaaziz – Academia.edu Cours et exercices de mathématiques SUITES ARITHMETIQUES ET GEOMETRIQUES EXERCICES CORRIGES. Cours et exercices de mathématiques SUITES ARITHMETIQUES ET GEOMETRIQUES EXERCICES CORRIGES
- Table of Contents:
People also downloaded these free PDFs
People also downloaded these free PDFs

exercice suite arithmétique pdf
- Article author: pierrelux.net
- Reviews from users: 20986
Ratings
- Top rated: 3.0
- Lowest rated: 1
- Summary of article content: Articles about exercice suite arithmétique pdf SUITES ARITHMÉTIQUES et SUITES GÉOMÉTRIQUES : exercices – page 1 http://pierrelux.net … Soit (un ) la suite arithmétique de 1er terme 3 et de raison 4. …
- Most searched keywords: Whether you are looking for exercice suite arithmétique pdf SUITES ARITHMÉTIQUES et SUITES GÉOMÉTRIQUES : exercices – page 1 http://pierrelux.net … Soit (un ) la suite arithmétique de 1er terme 3 et de raison 4.
- Table of Contents:

exercice suite arithmétique pdf
- Article author: www.gymomath.ch
- Reviews from users: 16959
Ratings
- Top rated: 3.4
- Lowest rated: 1
- Summary of article content: Articles about exercice suite arithmétique pdf Calculer la valeur de la plus petite des récompenses. Exercice 2.18 : Suite génétique. La suite définie par récurrence par xk+1 = xk. …
- Most searched keywords: Whether you are looking for exercice suite arithmétique pdf Calculer la valeur de la plus petite des récompenses. Exercice 2.18 : Suite génétique. La suite définie par récurrence par xk+1 = xk.
- Table of Contents:

exercice suite arithmétique pdf
- Article author: auriolg.free.fr
- Reviews from users: 10994
Ratings
- Top rated: 3.1
- Lowest rated: 1
- Summary of article content: Articles about exercice suite arithmétique pdf Suites – Exercices – Terminale STMG – G. AURIOL, Lycée Paul Sabatier. Suites – Exercices. Révision. 1 Soit la suite arithmétique de raison et de premier. …
- Most searched keywords: Whether you are looking for exercice suite arithmétique pdf Suites – Exercices – Terminale STMG – G. AURIOL, Lycée Paul Sabatier. Suites – Exercices. Révision. 1 Soit la suite arithmétique de raison et de premier.
- Table of Contents:

exercice suite arithmétique pdf
- Article author: www.jaicompris.com
- Reviews from users: 36191
Ratings
- Top rated: 3.8
- Lowest rated: 1
- Summary of article content: Articles about exercice suite arithmétique pdf Suite arithmétique – Premi`ere S ES STI – Exercices … Suite arithmétique – Déterminer la raison et calculer des termes. …
- Most searched keywords: Whether you are looking for exercice suite arithmétique pdf Suite arithmétique – Premi`ere S ES STI – Exercices … Suite arithmétique – Déterminer la raison et calculer des termes.
- Table of Contents:

exercices corrigés suites arithmétiques géométriques pdf
- Article author: www.etusup.org
- Reviews from users: 18832
Ratings
- Top rated: 4.5
- Lowest rated: 1
- Summary of article content: Articles about exercices corrigés suites arithmétiques géométriques pdf 5 exercices corrigés des suites arithmétique et géométriques, vous trouvez la correction sous forme PDF. …
- Most searched keywords: Whether you are looking for exercices corrigés suites arithmétiques géométriques pdf 5 exercices corrigés des suites arithmétique et géométriques, vous trouvez la correction sous forme PDF. 5 exercices corrigés des suites arithmétique et géométriques, vous trouvez la correction sous forme PDF
- Table of Contents:
Exercice 1
Exercice 2
Exercice 5
Correction
Télécharger
Voir aussi
1- exercices corriges algèbre2-Algèbre linéaire cours et exercices corrigés3-Exercices corrigés d’analyse integrales généralisées4-Exercices corrigés de les suite numérique5-Les matrices exercices corrigés6-Exercices corrigés de probabilité conditionnelle pdf
Membres
Exercice corrigé cinématique du point matériel pdf
cristallographie exercices corrigés pdf
optique géométrique exercices corrigés pdf
exercices corrigés suites arithmétiques géométriques pdf
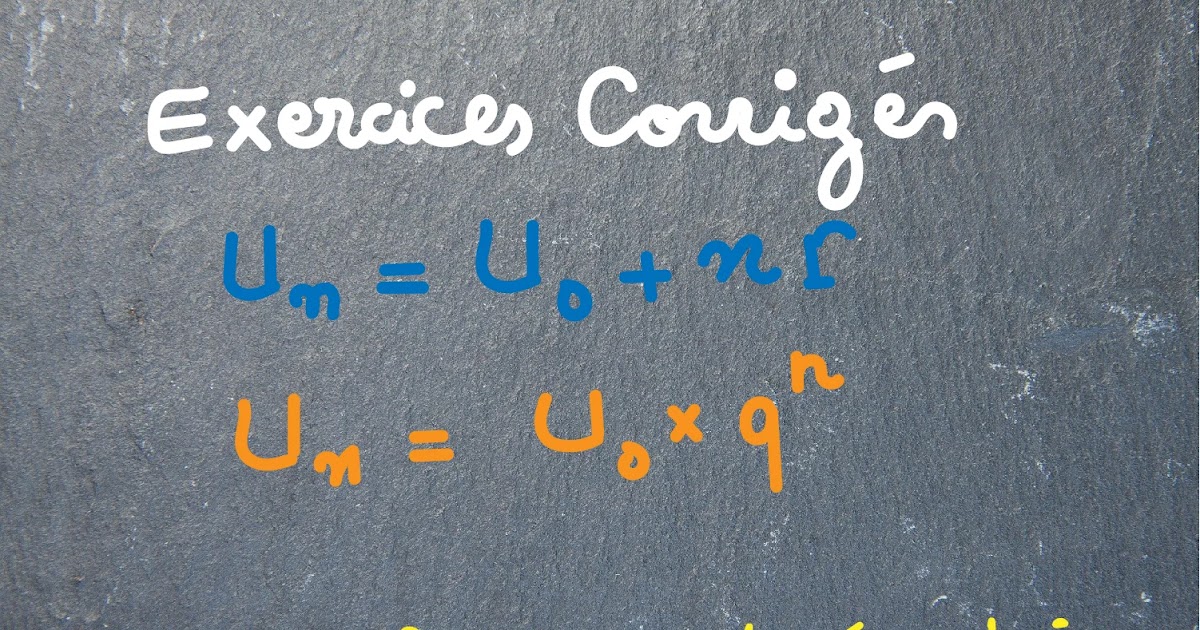
See more articles in the same category here: https://toplist.prairiehousefreeman.com/blog/.
Suites arithmetiques et géométriques
Cours maths 1ère S
Suites arithmetiques et géométriques
Suites arithmetiques et géométriques
Les suites
Les suites arithmétiques et les suites géométriques sont des suites particulières qui servent à modéliser bon nombre de situations de la vie courante.
Par exemple, les suites arithmétiques permettent de décrire l’amortissement des matériels informatiques achetés par une entreprise .
Les placements financiers avec taux d’intérêts ou les prêts bancaires sont modélisés avec des suites géométriques.
Suites arithmétiques
Définition :
Une suite est une suite arithmétique si et seulement si il existe un nombre réel r tel que, pour tout on ait
Si la suite est une suite arithmétique, le nombre réel r s’appelle la raison de cette suite.
Autrement dit, une suite est arithmétique si et seulement si chaque terme s’obtient en ajoutant au terme précédent un nombre réel r, toujours le même.
U n suite arithmétique ?
• Quelques points importants à retenir
Pour montrer qu’une suite est une suite arithmétique, il faut donc montrer qu’une suite est une suite arithmétique, il faut donc montrer qu’il existe un nombre réel r indépendant de n tel que, pour tout ,
Autrement dit, il faut montrer que la différence est constante :
Pour montrer qu’une suite n’est pas une suite arithmétique, il suffit de montrer que, sur les premiers termes par exemple, la différence n’est pas constante.
• Attention !
Pour montrer qu’une suite est une suite arithmétique, il ne suffit pas de vérifier que la différence est constante sur les premiers termes. Il faut le montrer pour tout entier n.
Exemples
1) La suite de tous les nombres entiers naturels est une suite arithmétique de premier terme 0 et de raison 1 :
2) La suite de tous les nombres entiers naturels pairs est une suite arithmétique de premier terme 0 et de raison 2 :
Expression du terme général en fonction de n
Remarque
Soit une suite arithmétique de raison r. Puisque, pour tout
le terme général est de la forme u n = ƒ(n)
ou ƒ est la fonction définie par ƒ(x) = u 0 + xr.
On peut donc calculer directement n’importe quel terme la suite.
De plus, comme la fonction ƒ est une fonction affine, une suite arithmétique de raison r est représentée dans le plan par des points alignés sur une droite de coefficient directeur r.
Représentation de la suite arithmétique de premier terme 0 et de raison 2 :
0, 2, 4, 6, 8……
Sens de variation d’une suite arithmétique
Soit une suite arithmétique de raison r. Alors on a, pour tout
On en déduit :
• Si r > 0, la suite est strictement croissante.
• Si r • Si r = 0, la suite est constante.
Somme des termes d’une suite arithmétique
Exemple fondamental
Calcul de la somme S n = 1 + 2 +…+ n
Avant de calculer cette somme rappelons l’anecdote relative au calcul de S100 par Gauss.
Carl Friedrich Gauss (30 Avril 1777 à Brunswick – 23 Février 1855 à Göttingen) fut non seulement un illustre mathématicien (il était surnommé « le Prince des mathématiques » ) mais aussi un physicien (il fit de nombreux travaux et publications en électricité, optique et magnétisme, théorie du potentiel) et un astronome réputé.
Un jour de 1786, à l’école primaire, le professeur qui voulait occuper ses élèves pendant un moment, leur demanda d’écrire tous les nombres de 1 à 100 et d’en calculer la somme.
Très peu de temps après, le jeune Carl Friedrich Gauss qui n’était âgé que de 9 ans alla le voir et lui montra sa réponse, 5050, qui était exacte.
Son professeur, stupéfait, lui demanda comment il avait fait pour trouver cette réponse aussi rapidement.
Suites géométriques
Définition :
Soit est une suite géométrique si et seulement s’il existe un nombre réel non nul q tel que, pour tout , on ait
Si la suite est une suite géométrique, le nombre q s’appelle la raison de cette suite.
U n suite géométrique ?
Autrement dit, une suite est géométrique si et seulement si chaque terme s’obtient en multipliant le précédent par un nombre réel q, toujours le même.
Pour montrer qu’une suite est géométrique, il faut donc montrer qu’il existe un nombre réel non nul q indépendant de n tel que, pour tout
Autrement dit, il faut montrer que le quotient est constant :
Pour montrer qu’une suite n’est pas géométrique, il suffit de montrer que, sur les premiers termes par exemple, le quotient n’est pas constant.
Suite géométrique
• Attention !
Pour montrer qu’une suite est géométrique, il ne suffit pas de vérifier que, le quotient est constant sur les premiers termes de la suite.
Il faut le montrer pout tout entier n.
Exemple
Expression du terme général en fonction de n
On a la propriété suivante :
Propriété :
Soit une suite géométrique de raison q
Alors,
Pour tout
Pour tout
Pour tout couple (n,p) d’entiers naturels,
Signe du terme général d’une suite géométrique
Soit une suite géométrique de raison q, où q ≠ 0.
On a u n = u 0 x qn.
• Si q > 0, alors un, est du signe de u 0 .
• Si q
Les termes de la suite sont, dans ce cas, alternativement positifs et négatifs : u n est du signe de u 0 si n est pair et un est de signe opposé à u 0 si n est impair.
Sens de variation d’une suite géométrique
Soit une suite géométrique de raison q, où q ≠ 0.
Nous avons vu que si q n’est donc pas monotone.
Supposons donc que q > 0.
Comme on a :
&bullet Si q > 1 et un > 0, c’est à dire u0 > 0, alors la suite est strictement croissante.
&bullet Si q > 1 et un est strictement décroissante.
&bullet Si 0 0, c’est à dire u0 > 0, alors la suite est strictement décroissante.
&bullet Si 0 est strictement croissante.
Remarque :
Ces résultats généraux sur le sens de variation d’une suite géométrique ne sont pas à apprendre mais il faut savoir les retrouver dans l’étude de cas particuliers.
Raison du suite arithmétique
Trouver la raison d’une suite arithmétique
Si l’on connaît n termes consécutifs d’une suite arithmétique de raison r, dont le premier est a, on peut déterminer facilement cette raison.
En effet, la formule `u_n = a + r ( n − 1)` donne : r × ( n − 1 ) = u n − a
d’où r = ( u n − a ) / ( n − 1 )
Formule de la raison d’une suite arithmétique
La raison d’une suite arithmétique, dont le premier terme `u_1` est égal à `a`, est donnée par la formule : `r = {u_n – a}/{n – 1}`.
Ce résultat signifie que, pour déterminer la raison, il faut retrancher au dernier terme le premier, puis diviser le résultat obtenu par le nombre de termes diminué de 1.
Cette règle permet de résoudre la question suivante :
Comment insérer un certain nombre de moyens différentiels entre deux nombres donnés ?
Cela revient à former une progression ayant pour premier et dernier terme, deux nombres donnés et un nombre de termes égal au nombre des moyens à insérer plus deux. Il s’agit donc de chercher la raison de cette progression.
Par exemple, insérer 7 moyens différentiels entre 3 et 4, c’est former une suite arithmétique de 9 termes dont le premier est 3 et le dernier 4.
La raison de cette suite est donc :
r = (4 − 3) / (9 − 1) = 1/8.
Les 9 termes de la suite sont :
u 1 = 3
u 2 = 3 + 1/8
u 3 = 3 + 2/8
…
u 8 = 3 + 7/8
So you have finished reading the exercice suite arithmétique pdf topic article, if you find this article useful, please share it. Thank you very much. See more: suites arithmétiques et géométriques exercices corrigés pdf, exercices corrigés suites arithmétiques pdf, exercice suite arithmétique corrigé, suite arithmétique exercice corrigé bac pro pdf, exercices corrigés suites terminale es pdf, exercices suites arithmétiques et géométriques 1ère, suite arithmétique exercice corrigé 1ere, somme suite arithmétique exercice corrigé
