You are looking for information, articles, knowledge about the topic nail salons open on sunday near me 아호 코 라식 on Google, you do not find the information you need! Here are the best content compiled and compiled by the https://toplist.prairiehousefreeman.com team, along with other related topics such as: 아호 코 라식 KMP 알고리즘, Aho-Corasick Python, 백준 9250, 트라이 알고리즘, C Trie, 라빈 카프 알고리즘
아호코라식(Aho-Corasick) : 네이버 블로그
- Article author: m.blog.naver.com
- Reviews from users: 27380
Ratings
- Top rated: 3.8
- Lowest rated: 1
- Summary of article content: Articles about 아호코라식(Aho-Corasick) : 네이버 블로그 아호코라식(Aho-Corasick)은 현재 광범위하게 알려진 거의 유일한 일대다 패턴매칭 알고리즘이고, 그 존재 자체만으로 거의 KMP급의, 개선의 여지가 … …
- Most searched keywords: Whether you are looking for 아호코라식(Aho-Corasick) : 네이버 블로그 아호코라식(Aho-Corasick)은 현재 광범위하게 알려진 거의 유일한 일대다 패턴매칭 알고리즘이고, 그 존재 자체만으로 거의 KMP급의, 개선의 여지가 …
- Table of Contents:
카테고리 이동
Ries 마법의 슈퍼마리오
이 블로그
대회알고리즘
카테고리 글
카테고리
이 블로그
대회알고리즘
카테고리 글
아호 코라식 알고리즘 – 위키백과, 우리 모두의 백과사전
- Article author: ko.wikipedia.org
- Reviews from users: 17394
Ratings
- Top rated: 4.0
- Lowest rated: 1
- Summary of article content: Articles about 아호 코라식 알고리즘 – 위키백과, 우리 모두의 백과사전 아호 코라식 알고리즘(Aho–Corasick string matching algorithm)은 Alfred V. Aho와 Margaret J. Corasick이 고안한 문자열 검색 알고리즘(매칭 알고리즘)이다. …
- Most searched keywords: Whether you are looking for 아호 코라식 알고리즘 – 위키백과, 우리 모두의 백과사전 아호 코라식 알고리즘(Aho–Corasick string matching algorithm)은 Alfred V. Aho와 Margaret J. Corasick이 고안한 문자열 검색 알고리즘(매칭 알고리즘)이다.
- Table of Contents:
키워드 트리[편집]
실패 링크[편집]
출력 링크[편집]
자료구조를 이용한 탐색[편집]
참조[편집]
[알고리즘] 아호 코라식(Aho-Corasick) 알고리즘
- Article author: pangtrue.tistory.com
- Reviews from users: 23696
Ratings
- Top rated: 5.0
- Lowest rated: 1
- Summary of article content: Articles about [알고리즘] 아호 코라식(Aho-Corasick) 알고리즘 2. 아호 코라식(Aho-Corasick) 알고리즘이란? · 일대다 문자열 패턴 매칭에 사용되는 알고리즘입니다. 패턴 문자열의 갯수와 상관없이 · 원본 문자열을 한 … …
- Most searched keywords: Whether you are looking for [알고리즘] 아호 코라식(Aho-Corasick) 알고리즘 2. 아호 코라식(Aho-Corasick) 알고리즘이란? · 일대다 문자열 패턴 매칭에 사용되는 알고리즘입니다. 패턴 문자열의 갯수와 상관없이 · 원본 문자열을 한 … 1. 개요 다음과 같은 두 개의 문자열이 있습니다. S = “abababdddd” (String의 약자를 따서 S라 표현) W = “bab” (Word의 약자를 따서 W라 표현) 아시는거처럼 S에서 W가 존재하는지를 찾아내는, 이른바 일대일..
- Table of Contents:
댓글
이 글 공유하기
다른 글
[자료구조] Trie(트라이) [알고리즘] KMP(Knuth-Morris-Pratt) 알고리즘 [알고리즘] 세그먼트 트리 (SegmentTree) [알고리즘] LIS(Longest Increasing Subsequence)티스토리툴바
![[알고리즘] 아호 코라식(Aho-Corasick) 알고리즘](https://img1.daumcdn.net/thumb/R800x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FbrSu9m%2Fbtq0nOFwhtB%2FC4pp9UTaycKO1I2ry1VjPK%2Fimg.png)
(C++) 문자열 검색 알고리즘 : 아호-코라식(Aho-Corasick) 알고리즘 – 평생 공부 블로그 : Today I Learned 🌙
- Article author: ansohxxn.github.io
- Reviews from users: 26956
Ratings
- Top rated: 4.5
- Lowest rated: 1
- Summary of article content: Articles about (C++) 문자열 검색 알고리즘 : 아호-코라식(Aho-Corasick) 알고리즘 – 평생 공부 블로그 : Today I Learned 🌙 아호 코라식 알고리즘을 이해하기 위해선 트라이 자료구조와 KMP 알고리즘 개념이 선행되어야 한다.(추가로 BFS 도 알고 있어야 한다.) … …
- Most searched keywords: Whether you are looking for (C++) 문자열 검색 알고리즘 : 아호-코라식(Aho-Corasick) 알고리즘 – 평생 공부 블로그 : Today I Learned 🌙 아호 코라식 알고리즘을 이해하기 위해선 트라이 자료구조와 KMP 알고리즘 개념이 선행되어야 한다.(추가로 BFS 도 알고 있어야 한다.) … 🚀 서론
- Table of Contents:
Skip links
🚀 서론
🚀 구현 코드 및 과정 설명
📌 Reference

[알고리즘] 다중 문자열 검색 아호 코라식(Aho-Corasick) 알고리즘 정리 (Java)
- Article author: loosie.tistory.com
- Reviews from users: 42189
Ratings
- Top rated: 4.2
- Lowest rated: 1
- Summary of article content: Articles about [알고리즘] 다중 문자열 검색 아호 코라식(Aho-Corasick) 알고리즘 정리 (Java) 아호 코라식 알고리즘(Aho–Corasick string matching algorithm)은 Alfred V. Aho와 Margaret J. Corasick이 고안한 문자열 검색 알고리즘(매칭 … …
- Most searched keywords: Whether you are looking for [알고리즘] 다중 문자열 검색 아호 코라식(Aho-Corasick) 알고리즘 정리 (Java) 아호 코라식 알고리즘(Aho–Corasick string matching algorithm)은 Alfred V. Aho와 Margaret J. Corasick이 고안한 문자열 검색 알고리즘(매칭 … Connecting The Dots
- Table of Contents:
아호 코라식(Aho-Corasick) 알고리즘
다중 문자열 검색
1 KMP 알고리즘으로 접근하기
2 트라이(Trie) 자료구조 적용하기
아호-코라식(Aho-Corasick) 문자열 검색 알고리즘 구현하기
시간 복잡도 분석
![[알고리즘] 다중 문자열 검색 아호 코라식(Aho-Corasick) 알고리즘 정리 (Java)](https://k.kakaocdn.net/dn/cIgyTc/btrmnmomZXE/WoKzasyxP4MKASNNE1mkr1/img.png)
Aho-Corasick Multiple Pattern Matching Algorithm
- Article author: koosaga.com
- Reviews from users: 12952
Ratings
- Top rated: 4.6
- Lowest rated: 1
- Summary of article content: Articles about Aho-Corasick Multiple Pattern Matching Algorithm Aho-Corasick Multiple Pattern Matching Algorithm … 문자열 S와 여러 개의 문자열 T가 주어졌을 때, T에 있는 문자열 중 하나와 S가 매칭이 되는 지를 … …
- Most searched keywords: Whether you are looking for Aho-Corasick Multiple Pattern Matching Algorithm Aho-Corasick Multiple Pattern Matching Algorithm … 문자열 S와 여러 개의 문자열 T가 주어졌을 때, T에 있는 문자열 중 하나와 S가 매칭이 되는 지를 … https://www.slideshare.net/ssuser81b91b/ahocorasick-algorithm 문자열 S와 여러 개의 문자열 T가 주어졌을 때, T에 있는 문자열 중 하나와 S가 매칭이 되는 지를 계산 할 수 있는 알고리즘이다. 선형 시간에 작..
- Table of Contents:
티스토리 뷰
티스토리툴바

아호코라식 다중 패턴 매칭(Aho-Corasick)
- Article author: coloredrabbit.tistory.com
- Reviews from users: 12617
Ratings
- Top rated: 4.3
- Lowest rated: 1
- Summary of article content: Articles about 아호코라식 다중 패턴 매칭(Aho-Corasick) 여러 문자열 패턴이 있고, 특정 문자열에 어떤 패턴이 어디에 존재하는지 확인하고 싶을 때 쓰는 알고리즘입니다. 기술적으로는 prefix와 suffix를 가지고 … …
- Most searched keywords: Whether you are looking for 아호코라식 다중 패턴 매칭(Aho-Corasick) 여러 문자열 패턴이 있고, 특정 문자열에 어떤 패턴이 어디에 존재하는지 확인하고 싶을 때 쓰는 알고리즘입니다. 기술적으로는 prefix와 suffix를 가지고 … 아호 코라식(Aho-chorasick) 여러 문자열 패턴이 있고, 특정 문자열에 어떤 패턴이 어디에 존재하는지 확인하고 싶을 때 쓰는 알고리즘입니다. 기술적으로는 prefix와 suffix를 가지고 노는 문자열 탐색 알고리즘..
- Table of Contents:
그냥 하는 노트와 메모장
아호코라식 다중 패턴 매칭(Aho-Corasick) 본문

KMP 알고리즘과 Aho-Corasick 알고리즘
- Article author: www.secmem.org
- Reviews from users: 40721
Ratings
- Top rated: 5.0
- Lowest rated: 1
- Summary of article content: Articles about KMP 알고리즘과 Aho-Corasick 알고리즘 본 글에서는 대표적인 문자열 검색 알고리즘인 KMP 알고리즘과 Aho-Corasick 알고리즘에 대해 다루려 한다. 두 알고리즘이 알고리즘계에서 잘 알려진 … …
- Most searched keywords: Whether you are looking for KMP 알고리즘과 Aho-Corasick 알고리즘 본 글에서는 대표적인 문자열 검색 알고리즘인 KMP 알고리즘과 Aho-Corasick 알고리즘에 대해 다루려 한다. 두 알고리즘이 알고리즘계에서 잘 알려진 … 본 글에서는 대표적인 문자열 검색 알고리즘인 KMP 알고리즘과 Aho-Corasick 알고리즘에 대해 다루려 한다. 두 알고리즘이 알고리즘계에서 잘 알려진 이유는 둘 모두 평균 시간 복잡도뿐 아니라 최악의 경우 시간 복잡도가 극적으로 개선되었기 때문이다. 두 알고리즘 모두 실제로는 다이나믹 프로그래밍의 한 예시일 뿐임에도 실제로는 어려운 알고리즘으로 생각되고 있었다. (내가 그랬다..) 풀고 싶은 문제 우리가 두 알고리즘을 이용해 풀고 싶은 문제는 아래와 같다. 1) 아주 긴 문자열 $S$ 와 짧은 문자열 $T$ 가 주어진다. $S$ 의 길이는 $N$,…
- Table of Contents:
풀고 싶은 문제
KMP 알고리즘
시간 복잡도
Aho-Corasick 알고리즘

Python에서 AhoCorasick(아호코라식) 알고리즘 구현하기
- Article author: tempdev.tistory.com
- Reviews from users: 40829
Ratings
- Top rated: 4.6
- Lowest rated: 1
- Summary of article content: Articles about Python에서 AhoCorasick(아호코라식) 알고리즘 구현하기 그래서 이 부분을 다중 패턴 매칭 알고리즘인 아호코라식을 사용하여서 구현하였다. 아호코라식 알고리즘은 찾아야 하는 패턴이 많을 때 단순 2중 for문에 … …
- Most searched keywords: Whether you are looking for Python에서 AhoCorasick(아호코라식) 알고리즘 구현하기 그래서 이 부분을 다중 패턴 매칭 알고리즘인 아호코라식을 사용하여서 구현하였다. 아호코라식 알고리즘은 찾아야 하는 패턴이 많을 때 단순 2중 for문에 … 지금 캐글에 논문을 입력으로 받아 논문에서 사용된 데이터셋 이름을 찾는 대회가 진행 중이다. 만약 알고 있는 데이터셋 이름이 있다면, 논문 속에서 그 이름을 단순 문자열 매칭을 이용해서 찾아내어서 출력에..
- Table of Contents:
태그
관련글
댓글0
공지사항
최근글
인기글
최근댓글
태그
전체 방문자
티스토리툴바

Aho-Corasick 알고리즘
- Article author: www.acmicpc.net
- Reviews from users: 43455
Ratings
- Top rated: 3.3
- Lowest rated: 1
- Summary of article content: Articles about Aho-Corasick 알고리즘 Aho-Corasick 알고리즘. 2015년 9월 29일; h0ngjun7; 댓글 (2개); aho-corasick, pattern-matching. Aho-Corasick Algorithm(아호 코라식 알고리즘) from Hongjun Jang … …
- Most searched keywords: Whether you are looking for Aho-Corasick 알고리즘 Aho-Corasick 알고리즘. 2015년 9월 29일; h0ngjun7; 댓글 (2개); aho-corasick, pattern-matching. Aho-Corasick Algorithm(아호 코라식 알고리즘) from Hongjun Jang … ACM-ICPC, ICPC, 프로그래밍, 온라인 저지, 정보올림피아드, 코딩, 알고리즘, 대회, 올림피아드, 자료구조
- Table of Contents:
Aho-Corasick 알고리즘
검색
최신 글
Baekjoon Online Judge
채점 현황
문제
유저 대회 고등학교 대회
출처
대학교 대회
도움말

See more articles in the same category here: https://toplist.prairiehousefreeman.com/blog/.
아호코라식(Aho-Corasick)
안녕하세요. 진짜 강좌를 이제 두 달만에… 메이플 개꿀잼이네요.
문자열 파트 글이 두 개 남았는데, 모두가 아실 아호코라식과 서픽스어레이입니다만…
오늘 드디어 제가 각 잡고 아호코라식 강좌글을 쓰려고 합니다.
아호코라식(Aho-Corasick)은 현재 광범위하게 알려진 거의 유일한 일대다 패턴매칭 알고리즘이고, 그 존재 자체만으로 거의 KMP급의, 개선의 여지가 보이지 않는 사기적 성능을 자랑합니다.
일대다 패턴매칭은 지금까지의 KMP나 라빈카프 등과 달리, 문자열 하나 안에 여러 각각의 문자열이 존재하는지를 다 판별하는 것을 말합니다.
문자열 S에서, 찾을 단어 집합 W의 각 단어 w1, w2, … , wk를 찾는다고 해봅시다. 그리고 S의 길이를 N, 각 단어의 길이를 m1, m2, … mk라 하면…
그냥 naive하게 완전탐색으로 찾는다면 O(N(m1+m2+…+mk))입니다.
그러나, 아호 코라식은 또 S를 한 번만 훑어서 결과를 내기 때문에 O(N+m1+m2+…+mk)입니다. (뭐???)
사실 저거보다는 좀 크긴 합니다. 전처리과정 및 기타등등 때문에… 하지만 여전히 대단한 건 사실.
KMP의 확장이 아호코라식이라고 볼 수 있습니다. 반대로 아호코라식의 축소가 KMP고요.
KMP와 유사하게, 오토마타적 개념이 들어갑니다. 한 번 예시를 봅시다.
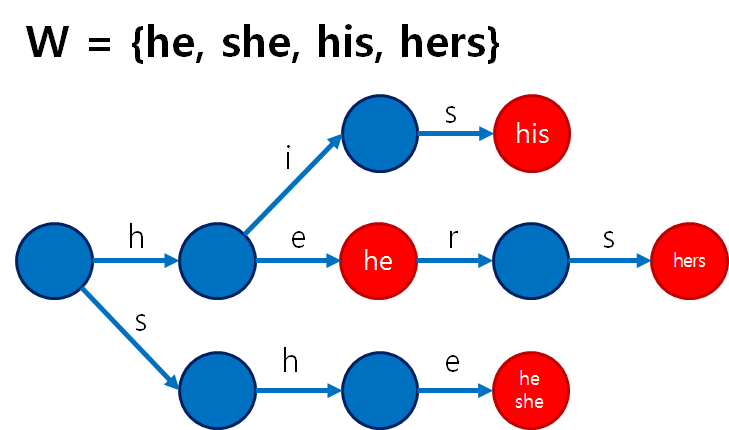
대략 이렇게 생겼는데 시작 state는 제일 왼쪽의 것입니다.
네, 이거… 바로 이전 글을 보셨다면 아시겠지만 일종의 트라이입니다.
여기서 S의 문자를 하나씩 인풋으로 읽어가면서 다음 state로 이동해야 하는데요. 다음 state를 go 함수로 정의합니다.
빨간 것들이 output 노드고, output 노드에 도달했다면 거기 적혀 있는 문자열들이 S에 등장한다는 것이 확정되는 겁니다.
output 노드들에는 이 노드를 지날 때 내뱉는 단어의 목록이 있는데 이를 output 함수라 합니다.
한 번 시뮬레이션을 해봅시다. S = “cdhisxy”일 때, 어떤 문자열들이 S에 들어있는지…!
현재 state가 빨간색입니다. 만약 중간에 매칭이 끊기면 시작 state로 돌아간다고 해보죠. 일단은…
일단 첫 번째 글자 c를 인풋으로 받아서 다른 데로 갈 수가 없네요. 그대로 있습니다.
다음 글자 d도 마찬가지입니다.
그러나 h를 보니까 이번엔 갈 수가 있네요. 이동합니다.
다음 글자인 i 역시 다음 길이 있으므로 이동.
s를 봐서 output 노드 중 하나에 도달합니다. 여기 도착했다면 “his”는 S에 속한다는 걸 알 수 있습니다.
직관적으로 맞고, 실제로도 맞죠. h, i, s를 순서대로 거쳐온 곳이 여기니까요.
그 다음 글자 x에 대한 이동경로가 없으므로 처음으로 돌아가고… 이하 생략.
일단 W의 원소를 찾는 걸 대략 살펴보았지만 아직은 뭔가 빠진 점이 있습니다.
일단 S를 앞에서부터 한 글자씩 훑어가다가 결과가 나와야 하고, 절대 뒤로 돌아가지 않는다는 원칙을 지켜야 하는데…
만약 S = “shis”라면 s, h를 지나고 i를 봤을 때 어디로 가야 할까요?
일단 S에 “his”가 있는 건 확실한데, i를 보고 시작지점으로 돌아가면 절대 저걸 찾을 수가 없습니다.
어디로 돌아가야 할까요?
일단 결과를 보고 끼워맞추기식으로 추측하자면, 시작지점에서 h를 받고 이동한 state로 보내야 “his”를 찾을 수 있습니다. 빨간색 점선으로 표시했습니다.
저기로 즉각 이동해서, 거기서 go(i)가 존재하는지 보고 존재한다면 이동하면 됩니다.
이렇게 아호코라식 알고리즘을 진행하면서 갈 곳이 없어지면 단순히 시작지점이 아니라 다른 어떤 곳으로 보내는 다른 함수가 필요합니다. 그것을 fail 함수라 칭합니다.
KMP에서도 사용했던 용어인데, 거의 비슷합니다. 여기선 저 오토마타가 일직선이 아닐 뿐이죠.
이렇게 아호코라식에는 go, output, fail 3개의 중요한 함수가 존재합니다.
그럼 이제 fail 함수 값을 도대체 어떻게 빠르게 알아내느냐가 문제입니다.
아무렇게나 알아내서 너무 느려지면 아호코라식의 저 빠른 탐색시간이 의미가 없어지니까요.
아니 일단 도대체 어디로 가야 할까요? 그것부터 알아봅시다.
위 예제에서, 왜 fail 함수 중 하나인 저 빨간 점선이 저렇게 이어져 있는 걸까요?
그것은 바로 그 state까지 거쳐온 인풋과 관련이 있습니다.
설명을 쉽게 하기 위해 몇몇 노드들에 이름을 붙이겠습니다.
여기서 go(u, h) = v, go(v, e) = w, go(u, s) = x이고
output(v) = {}, output(w) = {“he”},
fail(v) = u, fail(y) = v입니다. 이런 식으로 각 함수를 표기하겠습니다.
자 이제 fail(y) = v인 이유를 알아내야 하죠.
정점 y로 가려면 시작점으로부터 “sh”를 거쳐와야 하고, 좀 더 일반화하면 바로 최근에 훑은 문자가 s, h여야 합니다.
정점 v로 가려면 최근에 훑은 문자가 h기만 하면 될 겁니다.
한번 생각해 봅시다. W 집합 안에 h(…), sh(…) 2개의 단어가 있는데 (…) 부분이 동일하다고 해보죠.
그렇다면 만약 S에서 sh(…)를 찾았다면 자동으로 h(…)도 있어야만 합니다. 역은 성립하지 않죠.
따라서 sh(…)를 찾으러 가던 경로에서 어긋나도 h(…)로 가는 경로로 보내도 손해볼 게 없고, 오히려 다른 h로 시작하는 단어들, 여기서는 “his”를 문제없이 찾을 수 있을 겁니다.
또한, 그림에는 없지만 마찬가지 이유로 fail(z) = w이기도 합니다.
그러면 트라이상에 h가 엄청 많으면 어디로 보낼지 어떻게 아느냐? 여기서 규칙이 하나 더 있습니다. fail 함수는 반드시 자신보다 깊이가 작은 노드를 가리킵니다. 루트만 제외하고요.
어려운 예제를 한 번 봅시다. KMP에서 fail로 가고 또 거기서 fail로 가는 등, 한 번만 fail로 이동하고서 끝나지 않는 경우가 있는데, 아호코라식에서도 마찬가지입니다.
여기서도 그냥 루트로 가는 fail 간선들은 생략합니다. 그렇지 않은 것들에 대해 생각해보죠.
“ada” 노드에서의 fail은 쉽죠. “a”로 가면 될 겁니다.
만약 S = “adac”면 c를 보고 fail 함수를 통해 “a”로 돌아가 “ac”를 찾아갑니다.
노드 “adab”의 fail도 마찬가지로 노드 “ab”를 찾아가게 하면 됩니다. “adad”도 마찬가지로 “ad”로 보내면 됩니다.
지금까지 fail 함수를 관찰하면서 알 수 있는 점은, fail(x) = y면 x의 (x가 아닌) 접미사 중 하나가 반드시 y입니다. 그렇게 놀라운 사실이 아니죠? 그리고 이 말이 아까의 fail 함수 결과는 깊이가 줄어든다는 말을 뒷받침합니다.
여기서 더 나아가서, y는 가능한 한 가장 긴 접미사입니다. 다음을 봅시다.
몇몇 간선은 복잡해서 지웠고, “adada”의 fail이 “ada”가 되는데요.
자 이제 S = “adadac”면 마지막에 c를 보고 fail로 돌아가야 하는데요, 아직은 “ac”에 도달할 수 없죠.
여기서 한 번 더 fail을 타고 가보니 이제 go(…, c)가 존재합니다! “ac”를 찾을 수 있죠.
자, 이제 fail 함수가 주어졌을 때 메커니즘을 정리해 드리겠습니다.
① 현재 state x, 인풋 c에 대해 go(x, c)가 있으면 거기로 이동한다.
② 만약 없다면, fail(x)로 이동한 후 ①로 돌아간다. 단, 이미 루트면 아무것도 하지 않는다.
KMP를 어느 정도 이해하신 분이라면, 정말로 아호코라식이 KMP의 확장이 맞게 느껴지실 겁니다. 상당 부분이 비슷하게 작동하고 있죠.
이제 마지막으로 fail 함수를 정하는 것만 빠르게 하면 되겠는데요. 아까 말씀드렸듯이 fail(x)는 트라이상에 존재하는 x의 가장 긴 접미사 노드입니다. 물론 x 자신은 아닙니다.
이걸 찾아야겠는데… BFS를 통해 깊이가 작은 노드부터 방문해가면 fail 함수를 DP를 적용하듯이 결정할 수 있습니다.
아까 첫 번째 예제에서 “he”와 “she”를 보면, fail 함수 간선들이 평행선을 그리는데 이것 또한 그리 놀라운 일이 아닙니다.
만약 어떤 트라이상의 문자열 x, yx가 있고(x, y는 문자열) fail(yx) = x라 해봅시다. 그럼 여기에 각각 똑같은 문자열 z를 더 이어붙여 xz, yxz도 W에 포함시키면?
fail(yxz)는 무엇인가요? xz겠죠. 실제로 오토마타상에서 z 구간의 노드들의 fail을 다 간선으로 나타내면 쭈우우욱 평행선들을 그리게 될 겁니다.
이런 구조 덕분에, 문자열 p가 있을 때, 문자 x를 이어붙이면 fail(px) = go(fail(p), x)이 됩니다. 이제 바텀업 DP처럼 보이죠?
또한, 마지막으로 여기서 output 함수도 다듬어주어야 합니다. 사실 처음에 트라이를 만들 때 “she” 끝에 “he”도 속하는지 어떻게 알겠어요?
fail(x) = y일 때, output(y) ⊂ output(x)인 관계가 성립합니다! 이것도 접미사 관계에서 나타나는 관계죠.
이제부터 자세한 건 코드를 봅시다.
https://www.acmicpc.net/problem/9250
아호코라식 제일 기초 문제입니다. 노테이션에 주의해야 하는데 이 문제에서는 찾아야 할 단어의 집합이 S입니다.
Q번의 질문이 들어오는데 각 단어가 S의 원소를 적어도 하나 포함하는지를 대답하는 문제입니다.
아호코라식을 사용한다면 시간복잡도가 어떻게 되냐면, 오토마타를 만드는 데 O(S의 단어 길이 합), 각 단어 판정에 O(단어 길이)만큼이 들어갑니다. 후자 Q가 곱해졌을 시에 더 크고, 값이 대략 천만쯤 되므로 돌아갑니다.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 #include < cstdio > #include < queue > #include < algorithm > using namespace std ; // 트라이 구조체 struct Trie{ // 현재 노드에서 해당 문자를 받으면 가는 노드 Trie * go[ 26 ]; // 현재 노드에서 해당 문자의 go 목적지가 없을 때 가는 노드 Trie * fail; // 현재 노드에 도달하면 찾는 문자열 집합: 이 문제에서는 존재성만 따지면 됨 bool output; Trie(){ fill(go, go + 26 , nullptr); output = false ; } ~Trie(){ for ( int i = 0 ; i < 26 ; i + + ) if (go[i]) delete go[i]; } void insert( const char * key){ if ( * key = = '\0' ){ output = true ; return ; } int next = * key - 'a' ; if ( ! go[next]){ go[next] = new Trie; } go[next] - > insert(key + 1 ); } }; int main(){ int N, M; char str[ 10001 ]; // 트라이에 S의 원소들을 모두 집어넣는다. Trie * root = new Trie; scanf ( “%d” , & N); for ( int i = 0 ; i < N; i + + ){ scanf ( "%s" , str); root - > insert(str); } // BFS를 통해 트라이 노드를 방문하며 fail 함수를 만든다. queue < Trie * > Q; root – > fail = root; Q.push(root); while ( ! Q.empty()){ Trie * current = Q. front (); Q. pop (); // 26개의 input 각각에 대해 처리한다. for ( int i = 0 ; i < 26 ; i + + ){ Trie * next = current - > go[i]; if ( ! next) continue ; // 루트의 fail은 루트다. if (current = = root) next – > fail = root; else { Trie * dest = current – > fail; // fail을 참조할 가장 가까운 조상을 찾아간다. while (dest ! = root & & ! dest – > go[i]) dest = dest – > fail; // fail(px) = go(fail(p), x) if (dest – > go[i]) dest = dest – > go[i]; next – > fail = dest; } // fail(x) = y일 때, output(y) ⊂ output(x) if (next – > fail – > output) next – > output = true ; // 큐에 다음 노드 push Q.push(next); } } // 각 문자열을 받아 문제를 푼다. scanf ( “%d” , & M); for ( int i = 0 ; i < M; i + + ){ scanf ( "%s" , str); // 루트부터 시작 Trie * current = root; bool result = false ; for ( int c = 0 ; str[c]; c + + ){ int next = str[c] - 'a' ; // 현재 노드에서 갈 수 없으면 fail을 계속 따라감 while (current ! = root & & ! current - > go[next]) current = current – > fail; // go 함수가 존재하면 이동. 루트면 이게 false일 수도 있다 if (current – > go[next]) current = current – > go[next]; // 현재 노드에 output이 있으면 찾은 것이다. if (current – > output){ result = true ; break ; } } // 결과 출력 puts(result ? “YES” : “NO” ); } // 내 힙은 소중하기에 꼭 동적할당을 해제한다. delete root; } Colored by Color Scripter cs
코드가 크게 트라이 구조체 정의, 트라이에 S의 원소들 삽입, fail 및 output 함수 완성, Q개의 문자열 각각 판정하기 이렇게 4구간으로 나뉘어 있습니다.
매우 기니까 부분부분 쪼개서 보시는 걸 추천드립니다.
사실 위 코드에서는 항상 fail(x)가 x의 가장 긴 접미사가 아닐 수도 있는데요, 그건 굳이 그렇지 않아도 결과에 아무 영향이 가지 않아서입니다.
추천 문제
9250번: 문자열 집합 판별
위에서 설명한 문제입니다.
10256번: 돌연변이 (★)
BOJ에서 아호코라식 응용 문제 중 제일 유명합니다. 마커의 길이가 최대 100이니까, 그냥 가능한 모든 돌연변이 마커를 찾아 트라이를 구성하면 됩니다. 돌연변이 마커의 개수는 O(m^2)개죠. 그리고 주어진 DNA에서 몇 개의 단어가 등장하는지 세면 됩니다. 개수를 세려면 단순히 output이 bool 변수면 안 되겠죠?
트라이의 성격상 메모리를 굉장히 많이 쓰는데 한 입력에 테스트 케이스도 여러 개기 때문에, 자신이 만약 트라이나 무언가를 동적할당한다면 꼭 해제를 해주셔야 합니다. 또한 문자가 4개밖에 등장하지 않으므로 어떻게든 대응을 시켜 go 배열도 4칸으로 최소화하는 게 좋습니다. 메모리 초과가 많이 나는 문제입니다.
5735번: Emoticons (★)
아주 조금만 응용을 해야 합니다. 일단 이젠 영소문자만 등장하지가 않으므로 go 함수 메모리가 더 커질 겁니다. 각 문장마다 이모티콘을 한 번 찾을 때마다, 그 찾은 이모티콘의 제일 끝 자리에 대응하는 글자만 지우면 최소 개수의 글자를 지울 수 있습니다.
6300번: Word Puzzles
방법을 굳이 설명하지 않겠습니다… 여러분이 생각하시는 그게 맞을 겁니다… 정말 자신이 코딩변태다 싶은 분이 아니면, 그냥 이런 문제가 대회에 나온 적이 있구나 하는 정도만 알아가시는 게…
아호 코라식 알고리즘
아호 코라식 알고리즘(Aho–Corasick string matching algorithm)은 Alfred V. Aho와 Margaret J. Corasick이 고안한 문자열 검색 알고리즘(매칭 알고리즘)이다.
패턴 1개를 탐색하는 매칭 알고리즘은 선형 시간에 구현됨을 KMP 등 여러 알고리즘을 통하여 증명되었다. 하지만 패턴 집합에 대하여 이러한 알고리즘을 수행하게 되면 패턴 개수에 비례하여 그 속도가 느려지게 된다. 즉, O ( m + z n ) {\displaystyle O(m+zn)} 의 시간 복잡도를 가지게 된다.( m {\displaystyle m} : 모든 패턴들의 길이 합, z {\displaystyle z} : 패턴 수, n {\displaystyle n} : text 크기) 하지만 Aho-Corasick 알고리즘을 이용하면 O ( m + n + k ) {\displaystyle O(m+n+k)} 의 시간 복잡도로 패턴 집합에 대하여 패턴 길이와 텍스트의 선형 시간에 탐색을 처리할 수 있게 된다.(k: 텍스트 내에 패턴의 발생 수) 이러한 Aho-Corasick 알고리즘을 구현하기 위하여 Keyword Tree, Failure link, Output link 자료구조를 사용하여야 한다.
키워드 트리 [ 편집 ]
키워드 트리(Keyword Tree)는 패턴의 글자 하나를 하나의 간선으로 한다. 그리고 서로 패턴들의 접두사가 최대한 같을 때까지는 같은 정점으로 간선을 따라가고 글자가 달라지면 다른 간선으로 가도록 만들게 된다. 전 처리 과정에서 Keyword Tree를 만들면서 모든 패턴들의 길이의 합의 시간 복잡도 안에 만들 수 있게 된다.
실패 링크 [ 편집 ]
모든 패턴을 차례로 Keyword Tree에 넣은 이 후에는 이 Tree에 실패 링크(Failure link)를 추가해주게 된다. 루트에서 거리가 1인 정점들의 Failure link는 루트로 초기화한다. 그리고 거리가 2 이상인 정점들에 대해서 거리를 키워가면서 바로 앞 정점의 Failure link를 따라 가서 앞 정점과 해당 정점 사이의 간선에 해당하는 글자와 Failure link를 따라 간 정점의 글자가 같으면 그 정점으로 Failure link를 저장하게 되고 아니면 계속 Failure link를 따라가면서 처리하고 만약 루트가 나오면 해당 글자와 같은 거리가 1인 정점이 존재하면 거기로 Failure link를 저장하고 아니면 루트로 저장하게 된다. 위와 같은 방법으로 하게 되면 모든 패턴들의 길이의 합의 시간 복잡도 안에 모든 Failure link를 만들 수 있게 된다.
출력 링크 [ 편집 ]
여기에 패턴들 중에 다른 패턴의 substring이 존재하게 되면 패턴들을 탐색하지 못 할 때가 발생할 수 있다. 이를 막기 위하여 출력 링크(Output link)라는 자료 구조를 추가하게 된다. 각각의 패턴들이 끝이 나는 정점은 그 정점을 Output link로 가지게 된다. 그리고 다른 정점에서 Failure link를 따라 가서 패턴이 끝이 나게 되면 여러 단계의 Failure link를 무시하고 바로 그 정점으로 Output link를 연결해 주게 된다. 이를 하기 위하여 Failure link를 추가할 때, 같이 Failure link를 따라간 정점이 패턴의 끝이면 그 정점으로 Output link로 하고 그렇지 않으면 그 정점의 Output link를 가져옴으로 모든 패턴들의 길이의 합의 시간 복잡도 안에 처리가 가능하게 된다.
자료구조를 이용한 탐색 [ 편집 ]
텍스트의 글자와 Keyword Tree의 간선의 글자와 비교하면서 정점으로 내려가게 된다. 비교하면서 내려가면서 Output link가 존재하는지 확인을 계속 하고 Output link가 존재하면 패턴이 발생했음을 알려주게 된다. 또한 비교하다가 틀리게 되면 Failure link를 따라 가서 계속 글자를 비교해 주면서 탐색을 하게 된다. 이와 같이 탐색을 하게 됨으로 텍스트에 대하여 한번 확인하였으면 다시 확인하지 않게 되고 따라서 O ( m + n + k ) {\displaystyle O(m+n+k)} 의 시간 복잡도로 처리가 가능하게 된다.
참조 [ 편집 ]
[알고리즘] 아호 코라식(Aho-Corasick) 알고리즘
1. 개요
다음과 같은 두 개의 문자열이 있습니다.
S = “abababdddd” (String의 약자를 따서 S라 표현)
W = “bab” (Word의 약자를 따서 W라 표현)
아시는거처럼 S에서 W가 존재하는지를 찾아내는, 이른바 일대일 문자열 패턴 매칭 알고리즘으로는 KMP 알고리즘이 있습니다.
그런데 매칭에 사용될 패턴이 다음과 같이 여러 개라면 어떨까요? 🤔
S = “abababdddd”
W = {“bab”, “bd”, “ab”}
즉, 하나의 문자열 안에서 여러 개의 부분 문자열이 존재하는지 찾아내는 일대다 문자열 패턴 매칭이라면 어떻게 할 수 있을까요?
물론 W 집합 안의 문자열에 대해 하나씩 KMP 알고리즘을 돌려보는 방법도 가능합니다.
KMP 알고리즘의 시간 복잡도는 $O(n+m)$ 니깐,
P 집합 안의 문자열의 갯수가 k개라고 할때 KMP 알고리즘으로 일대다 문자열 패턴 매칭을 했을 경우의 시간 복잡도는..
$O(kn+m_{1}+m_{2}+…+m_{k})$ 입니다.
2. 아호 코라식(Aho-Corasick) 알고리즘이란?
예상하신대로 아호 코라식은 일대다 문자열 패턴 매칭에 사용되는 알고리즘입니다. 패턴 문자열의 갯수와 상관없이 원본 문자열을 한 번만 훑어서 찾아내기 때문에 시간 복잡도는 $O(n+m_{1}+m_{2}+…+m_{k})$ 입니다. ( KMP보다 놀라울정도로 빠른건 아닌거같은데… 🧐 )
어쨋든, 아호 코라식 알고리즘은 KMP 알고리즘의 확장이라고 볼 수 있습니다. (메커니즘이 비슷합니다).
KMP 알고리즘이 문자열과 문자열 간의 매칭이라면, 아호 코라식은 문자열과 트라이 간의 매칭입니다.
(아호 코라식을 배우시기 전에 KMP 알고리즘과 트라이 자료구조가 선행이 되어있어야 합니다..!)
다음과 같은 트라이가 있습니다. (S는 원본 문자열, W는 패턴 문자열 집합)
[그림 1] 트라이 모습S 문자열과 트라이 간의 패턴 매칭 과정을 살펴보겠습니다.
[그림 2] 트라이에서의 매칭 과정이어서 그 다음 문자인 b도 있기 때문에 똑같이 “abab” 라는 문자열을 찾을 수 있습니다. 문제는 그 다음인데요,
b 문자 다음은 a 문자인데 해당 문자는 없기 때문에 현재 노드를 가리키는 포인터가 롤백을 해야합니다.
[그림 3] 트라이에서 매칭 중 실패한 상황트라이에서 매칭을 하다가 매칭이 실패했을 경우 현재 가리키고 있는 지점을 다른 곳으로 이동시키는 함수를 fail 함수라고 부릅니다.
그럼 포인터를 어디로 이동시켜야할까? 매칭에 실패한 문자 전까지의 일치한 문자열에 대해 접두사와 접미사가 같은 지점입니다.
[그림 4] 매칭에 실패했을 땐 그 전까지 일치한 문자열의 접두사-접미사가 같은 지점으로 이동다음부터는 지금까지의 과정을 반복하면 되니 생략하겠습니다. 😉
매칭의 과정과 실패했을 때 어디로 이동해야하는지는 알겠는데.. 어떻게 저 지점으로 이동할 수 있을까요?
이 부분부터 조금 어려울 수 있는데 하나씩 살펴보겠습니다.
트라이는 Trie 안에 각 노드를 가리킬 TrieNode 타입 변수를 두는 식으로 만들었습니다. (어떤 식으로 구현하는가는 자유입니다.)
class Trie { TrieNode root = new TrieNode(true); // 메서드는 생략.. } class TrieNode { TrieNode[] child; TrieNode fail; // 실패했을 때, 이동해야할 지점을 가리킬 변수 boolean isEnd; // 완성된 문자열인지 표시 (일반적인 트라이에 나오는 개념입니다.) boolean isRoot; TrieNode(boolean isRoot) { child = new TrieNode[26]; // 알파벳 소문자만 있다고 가정하고 사이즈는 26 this.isRoot = isRoot; } // 메서드는 생략… }
다음으로, 실패 함수 코드를 살펴보겠습니다. 해당 함수의 역할은 위 TrieNode의 fail 변수의 값을 채워주는 것입니다.
그러기 위해선 트라이를 탐색해야하기 때문에 BFS 탐색이 사용됩니다.
// 실패 함수 (KMP로 비교를 하다가 실패했을 때의 이동해야할 지점을 정의한다.) // 일반적인 KMP 구현에서 getPi() 메서드에 해당한다. void failure() { Queue
q = new LinkedList<>(); trie.root.fail = trie.root; // root 회귀 q.add(trie.root); // 트리에 담긴 문자열에 대해 접두사-접미사가 동일한 것을 뽑아내야 한다. (BFS 이용) while (!q.isEmpty()) { TrieNode currentNode = q.poll(); // 알파벳 소문자만 있다고 가정하고 크기는 26 for (int i = 0; i < 26; i++) { TrieNode nextNode = currentNode.child[i]; if (nextNode == null) continue; if (currentNode.isRoot) { // root 자식 노드의 fail은 그들의 부모인 root 노드가 된다. nextNode.fail = trie.root; } else { TrieNode failure = currentNode.fail; while (!failure.isRoot && failure.child[i] == null) { failure = failure.fail; } if (failure.child[i] != null) { failure = failure.child[i]; } nextNode.fail = failure; } if (nextNode.fail.isEnd) { nextNode.isEnd = true; } q.add(nextNode); } } } 세팅이 끝났으면 마지막으로 문자열과 트라이 간의 KMP 알고리즘을 사용하는 코드는 다음과 같습니다. boolean kmp(String origin, TrieNode root) { TrieNode currentNode = root; boolean isFind = false; for (int i = 0; i < origin.length(); i++) { int idx = origin.charAt(i) - 'a'; while (!currentNode.isRoot && currentNode.child[idx] == null) { currentNode = currentNode.fail; } if (currentNode.child[idx] != null) { currentNode = currentNode.child[idx]; } if (currentNode.isEnd) { // 원본 문자열에서 패턴 문자열 하나를 찾았다면 isFind = true; } } return isFind; } 3. 참고자료 [1] m.blog.naver.com/PostView.nhn [2] www.slideshare.net/ssuser81b91b/ahocorasick-algorithm [3] koosaga.com/157
So you have finished reading the 아호 코 라식 topic article, if you find this article useful, please share it. Thank you very much. See more: KMP 알고리즘, Aho-Corasick Python, 백준 9250, 트라이 알고리즘, C Trie, 라빈 카프 알고리즘
